Interversion limite et intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
amstramgram
- Membre Naturel
- Messages: 58
- Enregistré le: 10 Avr 2009, 14:08
-
 par amstramgram » 10 Avr 2009, 14:19
par amstramgram » 10 Avr 2009, 14:19
bonjour à tous,
Je suis bloqué sur un problème d'interversion de limite et d'intégrale. Je cherche à calculer
dt)
ma fonction f est continue par rapport aux deux variables et tend vers 0 lorsque R tend vers l'infini pour presque tout t dans [0,1] (en fait, partout sauf en 0)
ma question est donc de savoir si je peux intervertir limite et intégrale... y aurait-il un théorème de convergence dominée pour des familles de fonctions non indexées par

(i.e. des suites) mais par
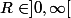
?
-
Arkhnor
- Membre Relatif
- Messages: 343
- Enregistré le: 05 Déc 2008, 20:02
-
 par Arkhnor » 10 Avr 2009, 14:31
par Arkhnor » 10 Avr 2009, 14:31
Salut.
Tu peux toujours utiliser le fait que une fonction f a une limite à l'infini ssi pour toute suite x_n tendant vers l'infini, f(x_n) tend vers la même valeur. (caractérisation séquentielle de la limite)
-
amstramgram
- Membre Naturel
- Messages: 58
- Enregistré le: 10 Avr 2009, 14:08
-
 par amstramgram » 10 Avr 2009, 15:35
par amstramgram » 10 Avr 2009, 15:35
Désolé mais je vois pas trop comment faire avec des suites...
mais pour la convergence dominée, qu'en est-il ? aurais-je le droit de considérer la famille de fonctions
)_{R\in]0,\infty[})
et d'écrire :
pour tout R, pour presque tout
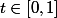
,
 \to 0)
pour tout R, pour presque tout t,
\right| \leq g(t))
avec g intégrable sur [0,1]
par conséquent,
dt=\int_0^1 \lim_{R\to\infty} f_R(t) dt = 0)
-
Arkhnor
- Membre Relatif
- Messages: 343
- Enregistré le: 05 Déc 2008, 20:02
-
 par Arkhnor » 10 Avr 2009, 16:19
par Arkhnor » 10 Avr 2009, 16:19
Ce que je te propose c'est justement de ramener ton problème ou R est un paramètre réel qui tend vers l'infini, à un problème où R_n est une suite tendant vers l'infini, et où le théorème de convergence dominée s'applique.
-
amstramgram
- Membre Naturel
- Messages: 58
- Enregistré le: 10 Avr 2009, 14:08
-
 par amstramgram » 10 Avr 2009, 16:49
par amstramgram » 10 Avr 2009, 16:49
ah je crois que je vois un peu mieux
Pour faire ça, il faut peut-être que je considère la suite de fonctions définie par
=f(R_n,t))
avec
)
une suite de réels > 0 qui tend vers l'infini quand n tend vers l'infini.
On a alors
dt = \lim_{n\to \infty} \int_0^1 f(R_n,t)dt)
et ensuite on conclue par convergence dominée appliquée à la suite f_n, c'est bien ça ?
Si c'est bel et bien ça, merci beaucoup, je devrais m'en sortir

-
Arkhnor
- Membre Relatif
- Messages: 343
- Enregistré le: 05 Déc 2008, 20:02
-
 par Arkhnor » 10 Avr 2009, 17:02
par Arkhnor » 10 Avr 2009, 17:02
On a en effet ça, à une subtilité près, c'est que tu dois le faire pour une suite quelconque R_n tendant vers l'infini et montrer que la limite ne dépend pas du choix de la suite, ce qui ne pose aucun problème ici. (je t'invite à relire ton cours de topologie si ça n'est plus tout à fait clair)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
