Intervalle d'un sous groupe discret

par **tristan** » 01 Juil 2006, 20:27

Bonjour quelqu'un pourrait-il m'aiguiller sur la solution de cet exercice ?

Soit (G,+,<) un groupe abélien totalement ordonné. On donne le nom d'intervalle à tous sous-ensemble I de G tel que si x et y appartiennent à I et x inférieur à y alors [x,y] est inclu dans I.

Montrer que si G est discret il existe un et un seul intervalle H de G qui possede la proprieté d'être un sous groupe isomorphe à (Z,+).

par **Killerboy** » 01 Juil 2006, 21:29

Je sais que c'est assez rudimentaire, pi que ça va p'tètre pas t'aider des masses, mais quand j'vois une démo avec existence et unicité, j'pense a une analyse-synthèse...
Après j'en ai aucune idée de comment la menée! :hein:

C'io ^^''

par **tize** » 02 Juil 2006, 10:31

Je suppose que

est un sous groupe strict de

. Ils sont tous de la forme

ou alors denses dans

Dans le premier cas c'est facile.

par **tristan** » 02 Juil 2006, 16:08

J'ai completé l'énoncé, G est un groupe abélien totalement ordonné. De plus G est [highlight]discret[/highlight]. Merci d'avance

par **Amine.MASS** » 02 Juil 2006, 16:39

bonjour,
je pense qu'il y a une erreur quelque part,en effet il y a des sous groupes de (IR,+) discret et dont aucune intervalle n'est inclu (c_a_d qu'il n'existe aucun intervalle qui est inclu dans G) :hein: :hein:
Par contre,si tu cherches la démonstration de : "tout sous groupe discret de (IR,+) est de la forme

" fait moi savoir
Cordialement,Amine

par **tize** » 02 Juil 2006, 17:45

Amine, relis la definition des intervalles de

de Tristan. Ce que tu dis est vrai en fait tout sous groupe discret de

est de la forme

et ne contient donc pas d'intervalle (d'interieur non vide) de

. Mais ce n'est pas ce que dit Tristan !

par **Amine.MASS** » 02 Juil 2006, 18:35

tize a écrit:Amine, relis la definition des intervalles de de Tristan. Ce que tu dis est vrai en fait tout sous groupe discret de est de la forme et ne contient donc pas d'intervalle (d'interieur non vide) de . Mais ce n'est pas ce que dit Tristan !

dsl :girl2: :briques:

par **tize** » 02 Juil 2006, 19:54

tristan a écrit:Montrer que si G est discret il existe un et un seul intervalle H de G qui possede la proprieté d'être un sous groupe isomorphe à (Z,+).

Peut être que je me trompe ou alors les données sont incomplètes mais si on prend

avec l'ordre lexicographique (c'est un groupe abélien totalement ordonné et discret) alors on a une infinité d'intervalles isomorphe à

par exmple : l'intervalle représenté par l'ensemble des éléments de la forme

Ou n'importe quel entier à la place de 0 convient.
Qu'en pensez vous ?

par **mathelot** » 02 Juil 2006, 21:11

G archimédien ?

par **tristan** » 02 Juil 2006, 22:47

Non il n'y a pas d'hypothese sur le carcatère archimedien. Ce qui fait que l'exemple

l'intervalle représenté par l'ensemble des éléments de la forme Ou n'importe quel entier à la place de 0 convient.

de Tize est bon, mais a priori seul 0 convient puisqu'on cherche à trouver un intervalle qui soit un sous groupe de G isomorphe à (Z,+).

L'énoncé est correct (Arnaudies-fraysse,T2).
Je crains que la redaction soit lourde, mais comme j'ai justemment du mal avec tout ce qui est isomorphismes (je n'arrive pas à en faire quelquechose de non abstrait) je suis reconnaissant d'avance à ceux qui trouveraient le temps de m'aider.

par **RadarX** » 02 Juil 2006, 23:11

Sans avoir lu toutes les contributions je voudrais d'ores et déjà preciser que G devrait etre discret et meme infini par hypothese pour qu'une partie (H) de G puisse etre isomorphe a (Z ; +).

par **RadarX** » 02 Juil 2006, 23:20

Amine.MASS a écrit:Par contre,si tu cherches la démonstration de : "tout sous groupe discret de (IR,+) est de la forme " fait moi savoir
Cordialement,Amine

Ben moi Amine, je veux bien de ta demo de cette affirmation qui me semble fausse: en effet je n'arrive pas (par exemple) à voir comment (Q ; +) qui est un sous groupe discret de (R ; +) s'ecrirait sous la forme aZ avec a >0!!!

Ce serait pareil pour (ID ; +) des decimaux!

par **nuage** » 02 Juil 2006, 23:24

Salut,
Il ne me semble pas que Q soit discret dans R.
Du moins pour la toplogie usuelle.

Ps : un groupe fini ne peut pas être muni d'un ordre total compatible avec la loi de groupe.

par **RadarX** » 02 Juil 2006, 23:29

nuage a écrit:Salut,
Il ne me semble pas que Q soit discret dans R.
Du moins pour la toplogie usuelle.

Ben que si Q est discret dans R. Disons meme discret tout court (cela ne depend d'aucune autre sur-structure).
Entendons bien, discret veut dire denombrable (autrement dit en bijection avec IN ou Z) ; ce n'est pas une propriété topologique!

par **nuage** » 02 Juil 2006, 23:43

Salut,
Je suis en complet désacord avec RadarX.
L'idée d'un ensemble discret totalement ordonné est qu'il n'y a rien entre deux valeurs consécutives ( un tel ensemble est en bijection avec une partie de N ou Z).

Plus généralement, si mes souvenir sont bons, un ensemble est discret si les singletons sont des ouverts.

par **tize** » 02 Juil 2006, 23:45

Je ne pense pas que discret signifie denombrable sinon on aurait dit denombrable mais c'est bien une propriété topologique : Un ensemble

est discret ssi toute partie de

est un ouvert. On peut dire ausse ssi tous les singletons sont des ouverts. Avec la topologie de

induite sur

(tout ouvert contient un intervalle) il semble bien que

n'est pas discret.

par **tristan** » 02 Juil 2006, 23:50

Dans le cas d'un groupe abélien totalement ordonné, discret veut dire qu'il existe un minorant a>0 de G*+

ajout :La definition "G discret ssi tout élement x est isolé" est plus claire en effet

par **tize** » 02 Juil 2006, 23:50

tristan a écrit:... l'exemple de Tize est bon, mais a priori seul 0 convient puisqu'on cherche à trouver un intervalle qui soit un sous groupe de G isomorphe à (Z,+).

Merci d'avoir corrigé mon erreur tristan.

tristan a écrit:Dans le cas d'un groupe abélien totalement ordonné, discret veut dire qu'il existe un minorant a>0 de G*+

OK Je viens de revoir la définition p.5

par **RadarX** » 03 Juil 2006, 00:03

ouh la la!! je l'avais l'oublié celle la, de definition topologique.
Je retire ce j'ai dit concernant la discretion sur cet exercice.
Desolé pour Nuage, Tize, tristan etc.

Mais maintiens quand meme qu'en theorie des ensembles, un ensemble discret n'est rien d'autre qu'un ensemble en bijection avec IN donc denombrable. Discret s'emploie aussi en analyse par opposition a continu. Ma confusion vient donc du fait que j'ai considéré qu'un groupe est avant tout un ensemble.
Encore une fois sorry!

par **tize** » 03 Juil 2006, 00:52

Je crois avoir un truc pour l'unicité :
Si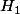

et

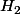sont deux sous groupe discrets de

alors alors ils ont chacun un plus petit élément >0 (resp.

et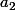

).

est totalement ordonné donc par exemple on

et comme

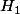et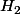

sont des intervalles contenant 0 (ce sont des sous groupes),

et donc

donc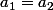

par définition de

.
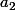Ensuite etant donné que ce sont des sous groupes isomorphes à

, on peut effectuer une division euclidienne pour constater que

Qu'en pensez-vous ?

Intervalle d'un sous groupe discret

Intervalle d'un sous groupe discret

Analyse synthèse?

Qui est en ligne