Groupe / Sous- groupe.

par **CDuce** » 08 Avr 2009, 17:33

Bonjours à tous ;
Alors voila j'ai un petit exercice au sujet des lois de compositions internes, (structures algébriques)
Soit (G,.) un groupe non commutatif, et G' un ensemble tel :

G'= {x£G / quelque soit a£G : ax=xa}

Montrer que (G',.) et un sous-groupe de (G,.) .

Alors pour répondre a cette question il faut trouver :
xy' £ G' (y' le symétrique de y) et bien sur G' non vide .

Pour (xy' £ G') voilà ce que j'ai fait : quelque soit x;y de G

a(xy')=(ax)y'=(xa)y'

Et puisque y£G et G est un groupe alors y'£G
Donc : ay'=y'a
Alors : (xa)y'=x(ay')=(xy')a

a(xy')=(xy')a ---> (xy') £ G' .

Alors est-ce-que ce raisonnement est juste, parce que j'ai un petit doute sur la partie en gras . Merci pour votre aide :]

par **Sve@r** » 08 Avr 2009, 18:17

CDuce a écrit:Bonjours à tous ;
Alors voila j'ai un petit exercice au sujet des lois de compositions internes, (structures algébriques)
Soit (G,.) un groupe non commutatif, et G' un ensemble tel :

G'= {x£G / quelque soit a£G : ax=xa}

Montrer que (G',.) et un sous-groupe de (G,.) .

Alors pour répondre a cette question il faut trouver :
xy' £ G' (y' le symétrique de y) et bien sur G' non vide .

Pour (xy' £ G') voilà ce que j'ai fait : quelque soit x;y de G

a(xy')=(ax)y'=(xa)y'

Et puisque y£G et G est un groupe alors y'£G
Donc : ay'=y'a
Alors : (xa)y'=x(ay')=(xy')a

a(xy')=(xy')a ---> (xy') £ G' .

Alors est-ce-que ce raisonnement est juste, parce que j'ai un petit doute sur la partie en gras . Merci pour votre aide :]

Niveau lycée ça ???

par **CDuce** » 08 Avr 2009, 18:33

Oui bien sur :d

par **Timothé Lefebvre** » 08 Avr 2009, 18:37

M'étonnerais, les structures et groupes ne sont pas vus au lycée (enfin pas ceux-là).

Direction le Sup'.

par **CDuce** » 08 Avr 2009, 18:43

Non mais je vous assure qu'on étudie ça en terminale =_=!
Les structures algébrique, l'espace vectoriel, enfin les lois internes et externes !!
Sinon c'est pas grave ;)

par **fati** » 08 Avr 2009, 18:54

tu suis quel programme? Maroc?

par **CDuce** » 08 Avr 2009, 19:02

Oui c'est ça :)

par **SimonB** » 08 Avr 2009, 19:06

Le raisonnement est juste (et le passage en gras est la partie centrale dudit).

par **leon1789** » 08 Avr 2009, 19:11

CDuce a écrit:Et puisque y£G et G est un groupe alors y'£G
Donc : ay'=y'a

ce "Donc" est non justifié.

"Quel que soit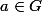

... "
"Quels que soient

... "
en 3 mots ;-)

par **CDuce** » 08 Avr 2009, 19:14

Ok d'accord, mais ce que je voudrai savoir le plus ; est-ce-que y'£G' pour mettre: ay'=y'a !? c'est vrai que x et y sont de G donc y' aussi ; mais pas forcement y'£G !!

par **leon1789** » 08 Avr 2009, 19:16

CDuce a écrit:c'est vrai que x et y sont de G donc y' aussi ; mais pas forcement y'£G !!

il faut démontrer que

implique

par **CDuce** » 08 Avr 2009, 23:03

Effectivement il faut s'assurer que y'£G' pour ensuite pouvoir mettre ay'=y'a !
Alors comment va-t-on le monter ?!

par **leon1789** » 09 Avr 2009, 08:14

Commence par écrire ya=ay ...

par **CDuce** » 09 Avr 2009, 13:00

Alors si on met : ay=ya

<=> ayy'=yay'
<=> a = y(ay') yy'=1 / (G,.) est un groupe ; e=1 ; la loi . est associative
<=> y'a=ay'
Donc y'£G' et puis après il faut montrer que (xy)£G' .
Merci beaucoup "leon1789" pour le coup de pouce ;)

Groupe / Sous- groupe.

Groupe / Sous- groupe.

Qui est en ligne