Intégrales curvilignes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 26 Avr 2008, 14:28
par rifly01 » 26 Avr 2008, 14:28
Bonjour,
J'ai un exercice à faire dont l'énoncé est :
[CENTER]

[/CENTER]
On avait défini le domaine
\in\mathbb{R}^{2}\mbox{ tel que }4x^2+y^2=k^2\Big\}$$)
et
\in\mathbb{R}^{2}\mbox{ tel que }4x^2+y^2\le k^2\Big\}$$)
2.
a) C'est du cours.
b) Soit

une forme différentielle de classe
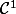
définie par
=-y\sqrt{4x^2+y^2}dx+x\sqrt{4x^2+y^2}dy=P(x,y)dx+Q(x,y)dy$$)
Alors
=-\sqrt{4x^2+y^2}-\frac{y^2}{\sqrt{4x^2+y^2}})
et
=\sqrt{4x^2+y^2}+\frac{4x^2}{\sqrt{4x^2+y^2}})
On a clairement

Or d'après la Formule de Green-Riemann on a aussi

c) La courbe d'équation
^2}+\frac{y^2}{1^2}=1)
sont l'ellipse de centre
)
d'axes
)
et
)
. On choisit donc comme paramétrage
 & = & 0+\frac{1}{2}\cos(t) \\ y(t) & = & 0+1 \sin(t) \end{array}\right.$$)
avec
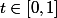
d) Calculons
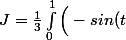\sqrt{4\times \frac{1}{4}\cos^{2}(t)+\sin^{2}(t)}\left(-\frac{1}{2}\sin(t)\right)+\frac{1}{2}\cos(t)\sqrt{4\times \frac{1}{4}\cos^{2}(t)+\sin^{2}(t)}\cos(t)\Big)dt=\frac{1}{3}\int_{0}^{1}\Big(\frac{1}{2}\sin^{2}(t)+\frac{1}{2}\cos^{2}(t)\Big)dt=\frac{1}{6})
Est-ce bon ? La rédaction est-elle correcte ? Pour une ellipse est-ce que le

du paramétrage varie-il toujours en

et

(mon idée c'est que

varie entre

et

). Ah,aussi. Le
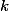
du domaine

représente quoi pour l'ellipse?
Merci d'avance,
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 26 Avr 2008, 14:54
par rifly01 » 26 Avr 2008, 14:54
Re,
Mon problème aussi. C'est que si je veux calculer

autrement, je ne tombe sur le même résultat.
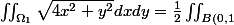}\sqrt{u^{2}+v^{2}}dudv =\int_{0}^{2\pi}\left(\int_{0}^{1}r^{2}dr\right)d \theta = \frac{1}{2}\frac{1}{3}2\pi = \frac{\pi}{3})
Changement de variable
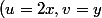)
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 26 Avr 2008, 17:31
par Maxmau » 26 Avr 2008, 17:31
rifly01 a écrit:Re,
Mon problème aussi. C'est que si je veux calculer

autrement, je ne tombe sur le même résultat.
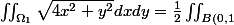}\sqrt{u^{2}+v^{2}}dudv =\int_{0}^{2\pi}\left(\int_{0}^{1}r^{2}dr\right)d \theta = \frac{1}{2}\frac{1}{3}2\pi = \frac{\pi}{3})
Changement de variable
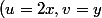)
Bj
Dans le paramétrage du contour, t varie de 0 à 2;) et non de 0 à 1
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 26 Avr 2008, 18:33
par rifly01 » 26 Avr 2008, 18:33
Bonjour,
Merci ça colle mieux avec ma l'autre méthode ! Merci
Sinon les autres réponses et leur rédaction ça va ?
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 26 Avr 2008, 19:25
par Maxmau » 26 Avr 2008, 19:25
rifly01 a écrit:Bonjour,
Merci ça colle mieux avec ma l'autre méthode ! Merci
Sinon les autres réponses et leur rédaction ça va ?
çà va très bien
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 26 Avr 2008, 20:01
par rifly01 » 26 Avr 2008, 20:01
Merci beaucoup,
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
 [/CENTER]
[/CENTER]