Intégrale d'une fonction dont on ne connait pas. possible ou
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 01 Mar 2012, 07:48
par Cryptocatron-11 » 01 Mar 2012, 07:48
Bonjour,
Existe t-il des fonctions qui admettent une intégrale sur un chemin qui va de a à b mais qui ne peuvent pas être explicitée ?
Je pose cette question car dans le cas des forces de frottement , on ne peut pas dire qu'elles dérivent d'une energie potentielle. En revanche
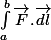
existe bien ....
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 01 Mar 2012, 12:22
par Skullkid » 01 Mar 2012, 12:22
Salut, je comprends pas ta question. Ça veut dire quoi "ne pas pouvoir être explicité" ? Et tu veux que ce soit la fonction elle-même qui ne puisse pas être explicitée, ou l'intégrale ?
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 01 Mar 2012, 13:27
par Cryptocatron-11 » 01 Mar 2012, 13:27
Skullkid a écrit:Salut, je comprends pas ta question. Ça veut dire quoi "ne pas pouvoir être explicité" ? Et tu veux que ce soit la fonction elle-même qui ne puisse pas être explicitée, ou l'intégrale ?
Une fonction qui ne peut pas être explicité c'est une fonction qu'on ne sait pas définir mais on sait qu'elle existe (vu qu'on a une intégrale) . On peut pas écrire f:x--> quelque chose par exemple.
Oui je veux que ce soit la fonction elle-même qui ne puisse pas être explicitée.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 01 Mar 2012, 14:00
par Skullkid » 01 Mar 2012, 14:00
Ça reste pas très clair pour moi... Pour qu'on puisse faire des calculs sur un objet, faut l'avoir défini auparavant. Mais on peut définir une fonction autrement qu'en écrivant une formule du genre f(x) = machin, on peut par exemple définir une fonction comme l'unique solution de telle équation différentielle avec telles conditions (la fonction exponentielle par exemple) ou comme la fonction réciproque de telle autre fonction. Et il est possible d'obtenir des renseignements sur une fonction (par exemple la valeur d'une certaine intégrale qui la fait intervenir) sans pour autant connaître parfaitement cette fonction.
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 01 Mar 2012, 14:05
par Cryptocatron-11 » 01 Mar 2012, 14:05
Ben dans le cas des forces de frottements. T'es bien d'accord qu'on peut calculer le travail le long d'un chemin. Le travail c'est une intégrale.
Est ce qu'on peut définir l'energie duquel dérive ces forces de frottement ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 01 Mar 2012, 14:27
par Skullkid » 01 Mar 2012, 14:27
Non, on ne peut pas définir d'énergie potentielle de frottement. Mais le fait que cette énergie n'existe pas n'a rien à voir ni avec l'existence ou non des forces de frottement, ni avec la possibilité ou non de calculer leur travail sur un chemin.
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 01 Mar 2012, 14:32
par Cryptocatron-11 » 01 Mar 2012, 14:32
Skullkid a écrit:Non, on ne peut pas définir d'énergie potentielle de frottement. Mais le fait que cette énergie n'existe pas n'a rien à voir ni avec l'existence ou non des forces de frottement, ni avec la possibilité ou non de calculer leur travail sur un chemin.
Ah ! bon , c'est bizarre d'un point de vue mathématiques. C'est un peu comme si on avait la dérivée sans la fonction ... Bref , ça doit être parce que c'est de la physique surement
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 01 Mar 2012, 15:41
par Judoboy » 01 Mar 2012, 15:41
Cryptocatron-11 a écrit:Ah ! bon , c'est bizarre d'un point de vue mathématiques. C'est un peu comme si on avait la dérivée sans la fonction ... Bref , ça doit être parce que c'est de la physique surement
J'avoue que je comprends pas bien ta question non plus, on connaît F, on l'intègre, où est le problème ? L'énergie dont dérive F c'est l'intégrale que tu as écrite au début...
En général connaître la dérivée sans connaître la fonction c'est pas si choquant que ça, regarde l'intégrale de Gauss : on n'a pas d'expression de la primitive de e^(-x²) à l'aide des fonctions usuelles, on peut juste écrire que c'est la primitive de e^(-x²).
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 01 Mar 2012, 16:14
par Billball » 01 Mar 2012, 16:14
certes tu peux intégrer, mais les forces de frottements dépendent du chemin suivi, donc non conservatives
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 01 Mar 2012, 16:54
par Cryptocatron-11 » 01 Mar 2012, 16:54
Judoboy a écrit:J'avoue que je comprends pas bien ta question non plus, on connaît F, on l'intègre, où est le problème ? L'énergie dont dérive F c'est l'intégrale que tu as écrite au début...
En général connaître la dérivée sans connaître la fonction c'est pas si choquant que ça, regarde l'intégrale de Gauss : on n'a pas d'expression de la primitive de e^(-x²) à l'aide des fonctions usuelles, on peut juste écrire que c'est la primitive de e^(-x²).
Bah au début, J'ai juste demandé si c'était possible et auquel cas me donner un exemple. J'ai pas dit que c'était impossible.
Après quand tu parle de dérivée d'une intégrale, es tu sur que c'est correcte? Une intégrale admet des dérivées ? Une intégrale c'est un nombre non ? Donc là par contre ce que tu viens de me dire me choque un peu.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 01 Mar 2012, 17:04
par Judoboy » 01 Mar 2012, 17:04
Je parlais de la primitive de e^(-x²) en fait. On ne peut pas l'expliciter sous une autre forme que "la primitive de e^(-x²), pourtant on connaît sa dérivée (qui est e^(-x²), thx captain obvious).
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 01 Mar 2012, 17:07
par Cryptocatron-11 » 01 Mar 2012, 17:07
Judoboy a écrit:L'énergie dont dérive F c'est l'intégrale que tu as écrite au début...
Non non mais moi je te parle de cette phrase ! Est elle correcte pour toi ?
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 01 Mar 2012, 17:13
par Judoboy » 01 Mar 2012, 17:13
Cryptocatron-11 a écrit:Non non mais moi je te parle de cette phrase ! Est elle correcte pour toi ?
Bah oui enfin tu dérives par rapport à b quoi, t'obtiens ta force.
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 01 Mar 2012, 17:18
par Cryptocatron-11 » 01 Mar 2012, 17:18
Judoboy a écrit:Bah oui enfin tu dérives par rapport à b quoi, t'obtiens ta force.
b est fixé

Et F n'est pas nulle
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 01 Mar 2012, 17:23
par Cryptocatron-11 » 01 Mar 2012, 17:23
En fait toi tu crois que j'ai posé F est fonction de b et que j'ai une intégrale indéfinie si je comprends bien ?
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 01 Mar 2012, 17:27
par Judoboy » 01 Mar 2012, 17:27
A vrai dire je sais pas trop, je trouve que ta question au départ n'a pas vraiment de sens.
Evidemment qu'on ne peut pas expliciter avec les fonctions usuelles n'importe quelle fonction intégrable.
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 01 Mar 2012, 17:41
par Cryptocatron-11 » 01 Mar 2012, 17:41
Judoboy a écrit:A vrai dire je sais pas trop, je trouve que ta question au départ n'a pas vraiment de sens.
Evidemment qu'on ne peut pas expliciter avec les fonctions usuelles n'importe quelle fonction intégrable.
Ah bon ? demander s'il existe des fonctions qui admettent une intégrale sur un chemin qui va de a à b mais qui ne peuvent pas être explicitée , ça n'a pas de sens pour toi ? Bah dans ce cas tes réponses non plus car je ne sais pas comment tu fais pour répondre à un truc dont tu penses qu'il n'y a pas de sens...
Par contre si on parle d'intégrale indéfini , il faut que ça soit continu sur l'intervalle où on se déplace. Il ne faut pas qu'il y ait de saut. Et donc
= \int_{a}^{b} F(t)dt +K)
c'est bien une fonction qui dépend de b. Et cette fonction , on ne peut pas l'expliciter à l'aide de fonction usuelle d'après ce que tu dis. C'est bien ce que tu voulais dire non ?
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 01 Mar 2012, 17:48
par Judoboy » 01 Mar 2012, 17:48
Cryptocatron-11 a écrit:Ah bon ? demander s'il existe des fonctions qui admettent une intégrale sur un chemin qui va de a à b mais qui ne peuvent pas être explicitée , ça n'a pas de sens pour toi ?
Ca a un sens mais la réponse est évidente, ça existe.
Bah dans ce cas tes réponses non plus car je ne sais pas comment tu fais pour répondre à un truc dont tu penses qu'il n'y a pas de sens...
Euuuuh ok....
Par contre si on parle d'intégrale indéfini , il faut que ça soit continu sur l'intervalle où on se déplace. Il ne faut pas qu'il y ait de saut.
Ah bon ? Tu ne sais pas intégrer une fonction en escalier ?
Et donc
= \int_{a}^{b} F(t)dt +K)
c'est bien une fonction qui dépend de b. Et cette fonction , on ne peut pas l'expliciter à l'aide de fonction usuelle d'après ce que tu dis. C'est bien ce que tu voulais dire non ?
Bah oui. Explicite-moi
= \int_{0}^{b} e^{-t^2}dt)
. Tu as 2 heures.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 01 Mar 2012, 17:50
par Sylviel » 01 Mar 2012, 17:50
Non d'un point de vue mathématique c'est très cohérent : si les forces de frottement dérivait d'une énergie alors leur travail serait le même quelque soit le chemin pris. Donc la force de frottement vérifie une ppté très particulière (grossièrement que son intégrale sur n'importe quel chemin fermé est nul)...
Les forces de frottement de vérifie pas cela !
Ton impression de "problème mathémtique" vient du fait que tu résonnes sur R et pas forcément sur R^2 ou plus grand...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 01 Mar 2012, 18:00
par Cryptocatron-11 » 01 Mar 2012, 18:00
Judoboy a écrit:Bah oui. Explicite-moi
= \int_{0}^{b} e^{-t^2}dt)
. Tu as 2 heures.
Le K n'a rien à faire là
Le K n'a rien à faire là ? Si jamais tu l'enlèves alors tu garde seulement LA primitive qui s'annule en a. Sauf quévidemment , y'en à pas qu'une. Pour info , on intègre toujours à une constante près.
Ah bon ? Tu ne sais pas intégrer une fonction en escalier ?
On peut donc intégrer une fonction pas continue sur un segment ? Comment fais tu pour intégrer la fonction 1/x^2 sur [0;+ infini[ ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
