Integrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cesc68
- Messages: 3
- Enregistré le: 09 Mar 2008, 21:11
-
 par Cesc68 » 09 Mar 2008, 21:13
par Cesc68 » 09 Mar 2008, 21:13
Bonjour j'aurais besoin de votre aide pour resoudre cette intégrale ( non bornée)
intégrale dx / 5+3cosx en posant u=tan(x/2)
le point de départ es je pense
du= 1/2 ( 1+u²) dx = 1/2 * (1/cos² (x/2)) dx
cos x = ( 1-u²) / ( 1+u² )
Merci de votre aide

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 09 Mar 2008, 21:16
par raito123 » 09 Mar 2008, 21:16
Y a t'il des intégrales non bornées??
Même pas par des fonctions??
Les multiples ne doivent pas être utilisés sans nécessité
-
Cesc68
- Messages: 3
- Enregistré le: 09 Mar 2008, 21:11
-
 par Cesc68 » 09 Mar 2008, 21:19
par Cesc68 » 09 Mar 2008, 21:19
ben par non borné j'entends qu'elle n'est pas définie

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 09 Mar 2008, 21:36
par raito123 » 09 Mar 2008, 21:36
Bon j'aime pas travailler sans borne du coup j'ai poser a et b comme borne ^.^
Rappel :

je trouve

par des calcul que tu dois faire tout seul : je trouve

Du coup c'est réglé
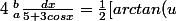]_{tg(a/2)}^{tg(b/2)})
à toi de faire les bons calculs :lol4:!!!
Les multiples ne doivent pas être utilisés sans nécessité
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Mar 2008, 21:40
par Nightmare » 09 Mar 2008, 21:40
Raito > C'est plutôt Arctan(u) entre crochet.
:happy3:

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 09 Mar 2008, 21:43
par raito123 » 09 Mar 2008, 21:43
Nightmare a écrit:Raito > C'est plutôt Arctan(u) entre crochet.
:happy3:
Réctifié!!
Les bornes aussi ! :lol4:
Les multiples ne doivent pas être utilisés sans nécessité
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Mar 2008, 21:48
par Nightmare » 09 Mar 2008, 21:48
Cela dit tu te compliques la vie avec les bornes, bien au contraire, quand on peut s'en passer, ne pas s'en priver!
-
Cesc68
- Messages: 3
- Enregistré le: 09 Mar 2008, 21:11
-
 par Cesc68 » 09 Mar 2008, 21:53
par Cesc68 » 09 Mar 2008, 21:53
mais pour le cos x je trouve
5 + 3 cos(x) = 5 + 3(1-u²)/(1+u²)
5 + 3 cos(x) = [5(1+u²) + 3(1-u²)]/(1+u²)
5 + 3 cos(x) = 2(4+u²)/(1+u²)
je vois pas trop ton explication

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 09 Mar 2008, 21:53
par raito123 » 09 Mar 2008, 21:53
Nightmare a écrit:Cela dit tu te compliques la vie avec les bornes, bien au contraire, quand on peut s'en passer, ne pas s'en priver!
Peut-on s'en passer des bornes?
Les multiples ne doivent pas être utilisés sans nécessité
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Mar 2008, 22:01
par Nightmare » 09 Mar 2008, 22:01
Oui bien sûr, cela veut dire qu'on travail sur les primitives (cela s'appelle une intégrale indéfinie)
Cesc68> Oui il a eu le 5+3cos(x) oublié mais tu auras compris la technique.

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 09 Mar 2008, 22:07
par raito123 » 09 Mar 2008, 22:07
Cesc68 a écrit:mais pour le cos x je trouve
5 + 3 cos(x) = 5 + 3(1-u²)/(1+u²)
je vois pas trop ton explication
C'est u²-1 (je pense) !!
Nightmare : j'ai oublier quoi?
Les multiples ne doivent pas être utilisés sans nécessité
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
