Intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
JCVD
- Messages: 8
- Enregistré le: 12 Oct 2019, 22:43
-
 par JCVD » 22 Oct 2019, 18:04
par JCVD » 22 Oct 2019, 18:04
Bonjour à tous!
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)
L'intégrale me posant problème est la suivante :
dx})
, où f : [0,1] ---> R
Comment résoudre cette intégrale?

-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 22 Oct 2019, 18:37
par Yezu » 22 Oct 2019, 18:37
Salut,
Considère la fonction
)
(quel est son ensemble de définition?). Étudie sa parité.
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 22 Oct 2019, 19:08
par LB2 » 22 Oct 2019, 19:08
moi je dirais : changement de variable u = -x
-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 22 Oct 2019, 20:24
par Yezu » 22 Oct 2019, 20:24
Salut,
@LB2, je ne suis pas sur, mais est-ce que ça revient au même ?
Dans le fond s'il utilise la propriété que l'intégrale d'une fonction impaire sur un intervalle symétrique p/r à 0 vaut 0.

-
jsvdb
- Membre Naturel
- Messages: 89
- Enregistré le: 20 Jan 2017, 09:45
-
 par jsvdb » 22 Oct 2019, 20:38
par jsvdb » 22 Oct 2019, 20:38
Yezu a écrit:Considère la fonction
)
(quel est son ensemble de définition?). Étudie sa parité.
Je considèrerais plutôt la fonction
)
sur
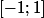
.
Bienheureux les fêlés car ils laissent passer la lumière !
-
sofianmakhlouf
- Membre Naturel
- Messages: 72
- Enregistré le: 03 Oct 2019, 15:54
-
 par sofianmakhlouf » 22 Oct 2019, 22:09
par sofianmakhlouf » 22 Oct 2019, 22:09
Bonsoir
l'intégrande est impaire

-
jsvdb
- Membre Naturel
- Messages: 89
- Enregistré le: 20 Jan 2017, 09:45
-
 par jsvdb » 22 Oct 2019, 22:17
par jsvdb » 22 Oct 2019, 22:17
Conclusion ?
Bienheureux les fêlés car ils laissent passer la lumière !
-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 22 Oct 2019, 22:46
par Yezu » 22 Oct 2019, 22:46
jsvdb a écrit: Yezu a écrit:Considère la fonction
)
(quel est son ensemble de définition?). Étudie sa parité.
Je considèrerais plutôt la fonction
)
sur
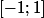
.
Salut,
Oui c'est pour l'intégrale direct, mon indication était surtout pour qu'il voit la parité de f(x^2) avant tout, car avec x c'est immédiat.

-
jsvdb
- Membre Naturel
- Messages: 89
- Enregistré le: 20 Jan 2017, 09:45
-
 par jsvdb » 22 Oct 2019, 22:47
par jsvdb » 22 Oct 2019, 22:47
Si c'est immédiat, alors autant faire d'une pierre deux coups
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)
Bienheureux les fêlés car ils laissent passer la lumière !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)

![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)

(quel est son ensemble de définition?). Étudie sa parité.
(quel est son ensemble de définition?). Étudie sa parité.
sur
.
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)