Intégrale et relation de récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
le fouineur
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Mai 2006, 10:21
-
par le fouineur » 13 Oct 2006, 13:11
Bonjour à tous,
Je cherche depuis longtemps une démonstration détaillée du calcul de l'intégrale suivante:
^ndx)
Après une intégration par parties,on trouve:
^n]_{-1}^{1}-2n\int_{-1}^{1}x.x(x^2-1)^{n-1}dx)
Et pour n>0
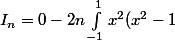^{n-1}dx)
Ensuite comment faire pour pouvoir conclure que:
???
Merci d'avance pour vos réponses,
Cordialement le fouineur
-
isortoq
- Membre Naturel
- Messages: 73
- Enregistré le: 28 Jan 2006, 20:54
-
par isortoq » 13 Oct 2006, 13:29
Il faut plutôt faire l'IPP à partir du produit (x+1)^n(x-1)^n...
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
par jose_latino » 13 Oct 2006, 13:34
Seulement il reste de faire une petite astuce:
^{n-1}dx=\int_{-1}^{1}(x^2-1+1)(x^2-1)^{n-1}dx=\int_{-1}^{1}((x^2-1)^{n}+(x^2-1)^{n-1})dx)
-
isortoq
- Membre Naturel
- Messages: 73
- Enregistré le: 28 Jan 2006, 20:54
-
par isortoq » 13 Oct 2006, 13:54
jose_latino a écrit:Seulement il reste de faire une petite astuce:
Oui, c'est vrai... En fait ce que je racontais permet de trouver la valeur explicite de
... qui s'appelle la formule de Rodrigues, si mes souvenirs sont bons... ce qui est loin d'être sûr !!!
-
le fouineur
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Mai 2006, 10:21
-
par le fouineur » 13 Oct 2006, 14:07
Bonjour à isortoq et à jose_latino et merci pour vos réponses rapides,
Bien vu pour jose_latino qui est le seul à me détailler l'astuce que je n'avais pas bien comprise....et sans laquelle on ne peut pas conclure l'exercice.
Cordialement le fouineur
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
