Integrale relation de chalse
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 19 Mar 2020, 16:37
par novicemaths » 19 Mar 2020, 16:37
Bonjour
Je souhaite comprendre la méthode de calcul de la relation de chalse avec les intégrales.
Soit la fonction
t=-8x^3-8x^2-8x+312)
Je dois calculer F définie par
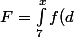t)
A bientôt
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 19 Mar 2020, 16:43
par GaBuZoMeu » 19 Mar 2020, 16:43
Relation de
Chasles, tu veux dire ???
C'est la relation
\,dt= \int_a^b f(t)\,dt+\int_b^c f(t)\,dt)
.
On te donne

, ce qui te permet de calculer

, et on te demande

. Facile, avec Chasles, non ?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 19 Mar 2020, 16:48
par novicemaths » 19 Mar 2020, 16:48
Oui!
On doit donc calculer une primitive ?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 22 Mar 2020, 15:12
par novicemaths » 22 Mar 2020, 15:12
Bonjour
Dois je commencer le calcul ainsi ?
t=\int_3^x f(d)t+\int_7^xf(d)t = [-2x^4-\frac{8}{3}x^3-4x^2+312x]_3^x+[-2x^4-\frac{8}{3}x^3-4x^2+312x]_7^x)
A bientôt
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Mar 2020, 15:29
par GaBuZoMeu » 22 Mar 2020, 15:29
Tu écris un peu n'importe quoi, là.
On te dit
\,dt=-8x^3-8x^2-8x+312)
Avec ça, il ne devrait pas être difficile de calculer
\,dt)
Puis après, appliquer la relation de Chasles pour obtenir

à partir de

et

-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 22 Mar 2020, 16:26
par novicemaths » 22 Mar 2020, 16:26
Je réessaie de poser l'opération.
t=-8x^3-8x^2-8x+312 =[-2x^4-\frac{8}{3}x^3-4x^2+312x]_3^7)
Est-ce qu'elle est posé.
A bientôt
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Mar 2020, 17:06
par GaBuZoMeu » 22 Mar 2020, 17:06
Tu t'embrouilles inutilement.
\,dt=-8x^3-8x^2-8x+312)
Tu as une égalité qui est valable pour tout réel
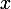
. Elle est en particulier valable pour

.
(En passant, tu peux vérifier qu'elle est bien valable pour

)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 22 Mar 2020, 17:33
par novicemaths » 22 Mar 2020, 17:33
Est-ce que la valeur de x=0 ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Mar 2020, 17:56
par GaBuZoMeu » 22 Mar 2020, 17:56

Vraiment, c'est trop difficile pour toi de remplacer
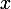
par 7 des deux côtés du signe = ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
