Intégrale à paramètre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sherman
- Messages: 2
- Enregistré le: 16 Déc 2017, 12:32
-
par Sherman » 16 Déc 2017, 12:37
Bonjour
Soit la fonction f(t,x)=
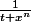
pour t>0 et x plus grand que 0.
Soit F(t)=
 dx)
(bien défini pour n plus grand que 2).
Montrer que F tend vers + infini quand t tend vers 0 (on pourra considérer une suite (tk) tel que tk tend vers 0 en décroissant (et toujours strictement positive))
En fait mon problème est que je n'arrive aps à dominer la fonction f(tk,x)
Merci
Cordialement
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 16 Déc 2017, 13:06
Salut,
Moi, mon problème, c'est que je vois pas ce que ça peut bien vouloir dire que
\!=\!\int f(t,x)\,dx)
sans précision concernant le domaine d'intégration.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Sherman
- Messages: 2
- Enregistré le: 16 Déc 2017, 12:32
-
par Sherman » 16 Déc 2017, 17:35
On intégre sur R+ (du coup c'est bien défini)
PS : n est entier fixé supérieur à 2.
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 16 Déc 2017, 18:01
Pour
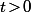fixé et tout
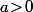
, tu as
=\int_{0}^{\infty}\dfrac{dx}{t+x^n}\geq\int_{0}^{a}\dfrac{dx}{t+x^n}\geq\int_{0}^{a}\dfrac{dx}{t+a^n}=\dfrac{a}{t+a^n})
Comment choisir le a (en fonction de t) pour que cette minoration soit la meilleure possible ?
Ca donne quoi comme minoration ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
