Intégrale à paramètre

[Trident]

Bonjour, j'ai une question sur un exo :

Soit la fonction définie pour tout t>0 par :


1. Montrer que F est bien définie et dérivable sur ]0,+oo[ et déterminer sa dérivée. Fait, on obtient :



2. Déterminer , n entier différent de 0.
J'ai justifié qu'on pouvait changer lim et intégrale et j'en ai déduit que :
.

3. Ensuite, c'est là ou je vois pas le rapport avec les questions précédentes :

"En déduire F(t) pour t > 0".

Merci de votre aide.

[Trident]

Je crois que j'ai une idée mais je vois toujours pas le rapport avec la question 2.

On remarque que F'(t) = t F(t) donc on en déduit F(t) = K . exp(-t²/2) avec K constante.

Après je me suis dit que la question 2 nous permettrait de déduire la constante K mais je ne vois pas...

[jlb]

Je crois que j'ai une idée mais je vois toujours pas le rapport avec la question 2.

On remarque que F'(t) = t F(t) donc on en déduit F(t) = K . exp(-t²/2) avec K constante.

Après je me suis dit que la question 2 nous permettrait de déduire la constante K mais je ne vois pas...

tu t'es planté dans ta dérivée dès le début!!!

[Trident]

Bonjour jlb. Pourquoi?

[jlb]

Bonjour jlb. Pourquoi?

pour le calcul de ta dérivée: tu différencies par rapport à la variable t et pas par rapport à x
ton prof est un blagueur, il a inversé le nom des variables par rapport aux énoncés "standarts" de ce théorème!!

[Trident]

Mais ma fonction de départ c'est une fonction qui a tout t > 0 associe le réel F(t) qui vaut l'intégrale de 0 à l'infini de exp(-tx) . sin(x)/x dx.

Autrement dit, si je note f(x,t) = exp(-tx) . sin(x)/t , je peux réécrire que ma fonction est celle qui a tout t>0, associe le réel F(t) = intégrale de 0 à l'infini de f(x,t) dx.

D'après le théorème de dérivation sous le signe somme, au final, je retrouve bien que :

F'(t) = intégrale de 0 à +oo de [dérivée par rapport à t de g(x,t)]dx

Je ne vois pas pourquoi ma dérivée n'est pas bonne.

[jlb]

Mais ma fonction de départ c'est une fonction qui a tout t > 0 associe le réel F(t) qui vaut l'intégrale de 0 à l'infini de exp(-tx) . sin(x)/x dx.

Autrement dit, si je note f(x,t) = exp(-tx) . sin(x)/t , je peux réécrire que ma fonction est celle qui a tout t>0, associe le réel F(t) = intégrale de 0 à l'infini de f(x,t) dx.

D'après le théorème de dérivation sous le signe somme, au final, je retrouve bien que :

F'(t) = intégrale de 0 à +oo de [dérivée par rapport à t de g(x,t)]dx

Je ne vois pas pourquoi ma dérivée n'est pas bonne.

oui mais tu t'es trompé, vérifie!!!

[Trident]

Ah oui !! C'est pas un "-t" mais un "-x" donc la dérivée vaut :



Donc du coup, c'est pire car je peux même pas rechercher une équa diff. Vois-tu le rapport avec la question 2 et 3 jlb ?

[Doraki]

Du coup tu peux trouver une primitive simple de l'intégrande dans l'expression de F'(t) ?

[jlb]

Ah oui !! C'est pas un "-t" mais un "-x" donc la dérivée vaut :



Donc du coup, c'est pire car je peux même pas rechercher une équa diff. Vois-tu le rapport avec la question 2 et 3 jlb ?

là, moi je simplifierai par x et je tenterai une intégration par partie deux fois de suite pour calculer effectivement F'.
( après tes deux intégrations tu doit retomber sur F' modulo un coefficient, tu regroupes les F' ensemble et tu trouves l'expression de F')
je ne te garantie rien, tu me diras si cela donne qlqchose?
En tout cas bon courage, je te laisse entre les mains de Doraki car tout cela me dépasse un peu

[Elizabet]

Ah oui !! C'est pas un "-t" mais un "-x" donc la dérivée vaut :



Donc du coup, c'est pire car je peux même pas rechercher une équa diff. Vois-tu le rapport avec la question 2 et 3 jlb ?

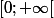
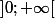
Si car est continue sur : et sur puis:
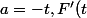est intégrable par parties. Si est une intégrale qui est définie d'où .

[Trident]

Du coup tu peux trouver une primitive simple de l'intégrande dans l'expression de F'(t) ?

En simplifiant, l'intégrande vaut -exp(-tx) sin(x). Je ne vois aucune primitive simple de cette quantité car ici la variable dedans l'intégrale, c'est x.

J'ai tenté une double IPP mais je retombe sur une égalité au finale I = I (avec I mon intégrale de départ), je vais retenter une double IPP en considérant les fonctions que je regardais comme des dérivées, comme des primitives mais bon...


Merci jlb pour ton aide.

[Doraki]

sin(x) et exp(x) (ou exp(tx)) c'est de la même famille. sinus, c'est une exponentielle déguisée.

sin(x) = partie imaginaire de exp(ix) par exemple, donc e^-tx sin(x), c'est partie imaginaire de e^((i-t)x), que tu devrais savoir intégrer.

Tu peux aussi dire que sin(x) = (e^ix-e^-ix)/2i et décomposer l'intégrale en 2 intégrales d'exponentielles.

Tu peux aussi chercher directement une primitive de la forme e^-tx(Acos(x)+Bsin(x)) avec A et B 2 constantes à déterminer. L'ensemble des fonctions de cette forme est un R-ev de dimension 2 stable par dérivation (ce qu'on vérifie aisément), la dérivation est linéaire et injective (puisque les constantes (à part 0) n'en font pas partie) donc surjective.

[Ben314]

Salut,
Je doit être un peu con (c'est même une certitude... :zen: ), mais dés le départ y'a un truc qui m'échape :
est sensée être convergente ?
c'est des intégrales au sens de quoi que vous manipulez : Riemann, Lebesgue, Stieltjes ?

EDIT : En fait c'est O.K. : c'est juste ce c... de TeX du site qui positionne les fractions n'importe comment...

[Doraki]

Même si dans code latex on voit bien que c'est (e^-tx) * sin(x) / x, la manière dont il l'écrit est effectivement traître, j'avais pas remarqué.

[Ben314]

Oui, je viens de voir : au départ j'ai rien compris, (et tapé mon post) puis en réfléchissant (comme quoi ça sert) je me suis dit "bon sûr, mais c'est bien sans" : il a fait une faute de frappe dans son accolade et je suis allé éditer son message et... même pas.... C'est juste l'affichage qui est "pas terrible..."

[jlb]

En simplifiant, l'intégrande vaut -exp(-tx) sin(x). Je ne vois aucune primitive simple de cette quantité car ici la variable dedans l'intégrale, c'est x.

J'ai tenté une double IPP mais je retombe sur une égalité au finale I = I (avec I mon intégrale de départ), je vais retenter une double IPP en considérant les fonctions que je regardais comme des dérivées, comme des primitives mais bon...


Merci jlb pour ton aide.

Essaie encore et vérifie bien tes calculs ç a fonctionne ( tu dérives sin puis cos dans tes IPP) si j'ai pas fait d'erreur tu tombes sur f'(t)=1/(1+t²) mais là c'est pas sur

[jlb]

bon, cela fonctionne avec double IPP ( tu dérives sin puis cos et tu retombes sur F' modulo un coefficient)
envoie tes calculs si t'es pas sur, bon courage.

[Trident]

En fait, la méthode de Doraki est pas mal avec le coup de la partie imaginaire, je pense qu'à partir de maintenant j'y penserai tout le temps.

Je trouve donc F'(t) = 1/(1+t²). Du coup, on en déduit que F(t)= arctan(t) (mais bizarre, quand je vérifie à la calculette je n'ai pas ça).

Mais je ne pense pas que le but de l'exercice était de trouver F(t) comme ceci. Il y avait "en déduire" dans la question 3, est-ce que quelqu'un voit le lien entre la 2 et la 3 ?

[jlb]

+ constante

En fait, la méthode de Doraki est pas mal avec le coup de la partie imaginaire, je pense qu'à partir de maintenant j'y penserai tout le temps.

Je trouve donc F'(t) = 1/(1+t²). Du coup, on en déduit que F(t)= arctan(t) + constante(mais bizarre, quand je vérifie à la calculette je n'ai pas ça).

Mais je ne pense pas que le but de l'exercice était de trouver F(t) comme ceci. Il y avait "en déduire" dans la question 3, est-ce que quelqu'un voit le lien entre la 2 et la 3 ?

euh et la constance d'intégration? c'est la question2), non?