Bonjour,
Voici un exercice sur lequel je bloque :
On pose f(r)= ∫ (de 0 à Pi) de ln( 1-2r cos(t) + r² ) dt
1) Vérifier que f est définie pour r appartenant à D=R\{-1,1}
2)Montrer que f est continue sur ]-1,1[
3)Montrer que f(r)=f(-r) pour r appartenant D
4)Trouver f(r²) en fonction de f(r) ainsi que f(1/r) en fonction de f(r)
5) Déduire des relations que f(r)=0 si r ∈ ]-1,1[ et f(r) = 2.Pi. ln(|r|) si |r|>1
6)Montrer que f est de classe C1 sur D et donner une expression intégrale de f'(r)
7)En déduire la valeur de ∫ (de 0 à Pi) de 1/(1-2r cos(t) + r²) dt, en utilisant r².f'(r)-f'(1/r)
J'ai fait les questions de 1,2,3,4
Je trouve f(r²) = 2 f(r)
et f(1/r) = f(r) + ∫ (de 0 à Pi) ln(1/r²) dt
Pouvez vous m'aider pour la 5
Merci d'avance
Intégrale a paramètre réel
3 messages
- Page 1 sur 1
Re: Intégrale a paramètre réel
salut
pourquoi ne finis-tu pas le calcul de f(1/r) en calculant l'intégrale ?
pourquoi ne finis-tu pas le calcul de f(1/r) en calculant l'intégrale ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Intégrale a paramètre réel
Salut,
Dans ton intégrale de la question 4, .
.
Pour la question 5, j'aurais dit que pour ,
, \rightarrow f(0) = 0) par continuité de
par continuité de  en
en  , et (par récurrence)
, et (par récurrence) =2^n f(r)) donc
donc =0) par passage à la limite.
par passage à la limite.
Pour le lien entre
le lien entre ) et
et ) te permettra de conclure puisque
te permettra de conclure puisque  =0) d'après ce qui précède.
d'après ce qui précède.
Je te confie la suite
Au passage, si tu fais de la physique tu pourras remarquer que tu obtiens à peu près l'équation du potentiel électrique pour un cylindre chargé en surface (pas évident à voir) : il est constant à l'intérieur du cylindre (ici il vaut mais bon il est défini à une constante près) et logarithmique à l'extérieur (ce qui se traduit par un champ électrique variant en
mais bon il est défini à une constante près) et logarithmique à l'extérieur (ce qui se traduit par un champ électrique variant en 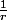 ).
).
Dans ton intégrale de la question 4,
Pour la question 5, j'aurais dit que pour
Pour
Je te confie la suite
Au passage, si tu fais de la physique tu pourras remarquer que tu obtiens à peu près l'équation du potentiel électrique pour un cylindre chargé en surface (pas évident à voir) : il est constant à l'intérieur du cylindre (ici il vaut
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
