Intégrale généralisée, transformée de Laplace
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
krafou
- Messages: 2
- Enregistré le: 11 Mar 2013, 22:44
-
par krafou » 11 Mar 2013, 23:02
Bonjour,
Je fais appel à votre aide car je suis bloqué depuis plusieurs jours sur le début d'un exercice.
est une fonction continue telle que pour tout entier naturel n,
)
tend vers 0 lorsque t tend vers
Je dois montrer que pour tout x supérieur ou égal à 0, l'intégrale généralisée
e^{-xt} dt)
est convergente.
Je ne sais pas comment m'y prendre, j'ai exploré plusieurs pistes (quantité de papier froissé) sans les mener à bien. J'aurais vraiment besoin de conseils pour m'aiguiller dans la bonne direction.
Merci d'avance.
-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
par alm » 11 Mar 2013, 23:19
Salut :
krafou a écrit:Bonjour,
Je fais appel à votre aide car je suis bloqué depuis plusieurs jours sur le début d'un exercice.
est une fonction continue telle que pour tout entier naturel n,
tend vers 0 lorsque t tend vers
Je dois montrer que pour tout x supérieur ou égal à 0, l'intégrale généralisée
est convergente.
Je ne sais pas comment m'y prendre, j'ai exploré plusieurs pistes (quantité de papier froissé) sans les mener à bien. J'aurais vraiment besoin de conseils pour m'aiguiller dans la bonne direction.
Merci d'avance.
Tu as à démontrer la convergence d'une intégrale impropre . Le problème est uniquement en
car
est continue en
.
On va donc discuter ce qui se passe au voisinage de
.
Soit
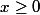
, alors, compte tenu des hypothèse et prenant
par exemple, on a :
 e^{-xt}|=0)
donc au voisinage de
, on a
e^{-xt}| = o \left(\frac 1{t^2} \right).)
Comme l'integrale de Riemann
est convergente , on en déduit la convergnece de
e^{-tx} dt.)
-
krafou
- Messages: 2
- Enregistré le: 11 Mar 2013, 22:44
-
par krafou » 12 Mar 2013, 00:11
Merci beaucoup ! Je tournais vraiment en rond. Tout me semble bien plus clair à présent.
-
aliquod
- Messages: 1
- Enregistré le: 25 Mar 2013, 22:32
-
par aliquod » 25 Mar 2013, 22:40
MOHAMED_AIT_LH a écrit:Salut :
Tu as à démontrer la convergence d'une intégrale impropre . Le problème est uniquement en
car
est continue en
.
On va donc discuter ce qui se passe au voisinage de
.
Soit
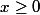
, alors, compte tenu des hypothèse et prenant
par exemple, on a :
donc au voisinage de
, on a
Comme l'integrale de Riemann
est convergente , on en déduit la convergnece de
Bonjour,
J'aurais voulu savoir comment vous déduisez la convergence de
du fait que
est convergente, car ce n'est pas le même intervalle d'intégration. Existe-t-il un théorème qui permet de l'affirmer ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
