Intégrable ?

[seballever]

Après moult recherches peu fructueuses pour savoir comment démontrer qu'une fonction est intégrable, me voilà toujours bredouille... la composée, le produit, la somme de fonctions intégrables sont intégrables ? et si on calcule l'intégrale d'abord (donc que ça marche... !) c'est bon ? merci de me faire avancer...

[klevia]

Salut,
Déja toutes fonctions continues sur un compact est intégrable sur ce compact.
Le problème vient surtout dans ce qu'on appelle les intégrales généralisées.
De manière générale on procéde par comparaison ou équivalent

sur un intervalle qcq
Ex: si f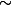g et si g intégrable alors f intégrable.

si f et g continue et (rajout) positive , f<g , et g intégrable alors f intégrable.

Maintenant pour les intégrales classique y'a surtout celle de Riemann et de bertrand

[ThSQ]

démontrer qu'une fonction est intégrable

Riemann-intégrable ? Lebesgue-intégrable ?


>>> si f et g positive , f<g , et g intégrable alors f intégrable.

C'est faux dans le cas de Riemann.

[klevia]

Ah bon ?
aurais-tu un contre exemple avec f et g continue, stp ?
merci

[quinto]

[quote]la composée[/b]

Non c'est clairement faux, la composée de fonctions intégrables n'est pas nécessairement intégrable.

[quinto]

Ah bon ?
aurais-tu un contre exemple avec f et g continue, stp ?
merci

Avec g et f continue, ca ne fonctionnera pas puisque les fonctions continues sont intégrables au sens de Lebesgue.

Si tu veux un exemple, il suffit de prendre f non Riemann intégrable.

En fait, il faudrait deja s'accorder sur le terme d'intégrabilité.
Veut on que les fonctions aient une intégrale sur certains ensemble, ou veut on dire que les fonctions sont d'intégrale de module finie ?

[ThSQ]

Ah bon ?
aurais-tu un contre exemple avec f et g continue, stp ?
merci

Avec f et g continues non bien sûr. Il suffit de prendre f non R-intégable dans le cas général.

[klevia]

Ouf, je me suis dit je ne comprends plus rien ...
mais c'est vrai que je n'ai pas été assez précise en oubliant de préciser f et g continue ....

je le rajoute de suite ...