Injectivité

[Momodu068]

Bonjour , j'aurais une question par rapport à l'injectivité.
En effet , dans un exercice on me demande de prouver une inégalité (que j'ai réussi à prouvé) qui est :
|e^s-e^t | > |(s-t) | pour tous s,t >0 puis on me dit d'en deduire que f est injective sur Ω ou Ω={ x>0,y>0} un ouvert et f : Ω dans R^2 ou f(x,y)=(e^x+y , e^y+x).

J'ai posé f(x1,y1)=f(x2,y2) et j'ai simplifié pour avoir d'un coté les exponentielles et de l'autre les variable y1 y2 mais je ne vois pas comment utiliser l'inegalité pour montrer que c'est injective merci d'avance !

[GaBuZoMeu]

Bonjour,
Premièrement, l'inégalité que tu as montrée est bien une inégalité large, n'est-ce pas ? Tu as écrit une inégalité stricte, alors que si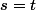 on a bien sûr égalité.
Ensuite, peux-tu écrire le système d'équations que te donne ?

[Momodu068]

Merci pour t'a réponse dans l'énoncé c'etait une inégalité stricte mais c'est vrai que cela marche également pour une inégalité large.
Pour le systeme j'obtient : e^x1+y1=e^x2+y2 et e^y1+x1=e^y2+x2
En regroupant j'ai : e^x1-e^x2=y2-y1 et e^y1-e^y2=x2-x1

[GaBuZoMeu]

C'est surtout qu'avec une inégalité stricte c'est faux !!!
À moins que tu aies oublié de nous dire que dans l'énoncé il est écrit "pour tous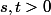 tels que "
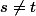Tu dis avoir mis les exponentielles d'un côté et le reste de l'autre. Peux tu le faire ?

[Momodu068]

Dans l'énoncé il est simplement écrit que s,t>0 comme je l'ai écris plus haut

En regroupant j'ai : e^x1-e^x2=y2-y1 et e^y1-e^y2=x2-x1

[GaBuZoMeu]

Alors l'énoncé est faux. Tu vois bien pourquoi ?
OK, je n'avais pas vu la dernière ligne. Peux-tu alors écrire les inégalités que tu as entre les différents côtés gauches et droits de tes équations ?

[Momodu068]

effectivement je vois pourquoi , pour écire l'equations avec les inégalités je voie pas trop comment faire car dans l'inegalité c'est avc des valeurs absolues

[Momodu068]

ok je crois que j'ai y2-y1≥ x1-x2 et x2-x1≥ y1-y2