Inégalité stricte en une inégalité large

[SaraHasbell]

Bonjour
je voudrais savoir comment transformer une Inégalité stricte en une inégalité large, voici un exemple :
puisque les nombres comparés sont des entiers, on a:
4(n^2+n) < p
qui devient:
4(n^2+n) + 1 <= p

[infernaleur]

Salut,
soit x,y des réels,

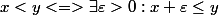
[pascal16]

un nombre entier strictement plus petit que 5 est inférieur ou égal à4.

soit x entier
x<5
<=> x ≤ 4
<=> x+1 ≤ 5

tu généralises ensuite

[Archytas]

De manière terre-à-terre

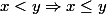
Donc pour transformer une inégalité stricte en large, tu rajoutes une petite barre sous ton inégalité stricte. C'est légal.
Si t'as question est "comment le faire de manière optimale ?" c'est impossible de te répondre en toute généralité. Ça dépend des cas.

[pascal16]

je pense que tu n'a pas vu le "+1" dans l'inégalité et le "nombre entiers".

[Archytas]

La question est posée sans conditions donc je réponds dans la plus grande généralité.
À lire ce qui est écrit j'ai l'impression que le cas "entier" est déjà compris et que la question est bien en toute généralité.

[pascal16]

1) "...les nombres comparés sont des entiers, on a:..."
2) ta réponse est juste mais ne correspond pas à la question

[Archytas]

C'est facile de faire dire tout et n'importe quoi en coupant les phrases où bon nous semble. Mais puisque je suis un crétin je laisse aux savants le soin d'interpréter et de répondre correctement aux questions.
Bisous