J'ai un système de cascade des équations de la chaleur suivant:
ou
on dénote
on a la fonctionnelle
ou
comment on démentrer que
Merci d'avance à votre aide. :happy2:
Convexité stricte d'une fonctionnelle
1 message
- Page 1 sur 1
convexité stricte d'une fonctionnelle
par White dove » 28 Mai 2009, 14:08
Bonjour à tous
J'ai un système de cascade des équations de la chaleur suivant:
=0 dans Q, \\<br />u=0 sur \Sigma,\\<br />u(x,0)=y_{0}(x) dans \Omega.<br />\end{array}<br /><br />\begin{array}{ll}<br />-\partial_{t}y-\Delta y+a(x,y)y=u1_{\mathcal{O}} dans Q ,\\<br />y=0 sur \Sigma,\\<br />y(x,T)=0 dans \Omega.<br />\end{array})
ou)
, et les ensembles ouverts non vide 
sont donnés dans 
, un ensemble ouvert borné connexe avec la frontière 
on dénote)
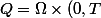et )
.
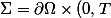on a la fonctionnelle
=\frac{1}{2}\int_{0}^{T}\int_{\omega}y^{2}dx<br />dt+\int_{0}^{T}\int_{\Omega}\xi y dx<br />dt+\epsilon\|u_{0}\|_{L^{2}(\Omega)})
ou)
, et)
est la solution du système linéaire précédent.
comment on démentrer que)
est strictement convexe?
Merci d'avance à votre aide. :happy2:
J'ai un système de cascade des équations de la chaleur suivant:
ou
on dénote
on a la fonctionnelle
ou
comment on démentrer que
Merci d'avance à votre aide. :happy2:
1 message
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :