Inégalité de Hölder
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Irrot
- Membre Naturel
- Messages: 15
- Enregistré le: 25 Fév 2017, 18:08
-
 par Irrot » 03 Mar 2017, 19:46
par Irrot » 03 Mar 2017, 19:46
Hello,
je dois démontrer que

ce pour tt x et y dans Rn et avec

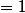
avec la convention que si p =1 alors l'autre est égal à l'infini. Par definition:
^{\frac{1}{p}})
et

ensuite le corrigé dit:
Par l’inégalité triangulaire pour la valeur absolue nous dérivons l’inégalité
de base:
 Il en suit directement l’inégalité de Hölder pour p = 1 i.e:
Il en suit directement l’inégalité de Hölder pour p = 1 i.e: 
Et je ne comprend pas en quoi cela prouve l'égalité... je sais ça à l'air débile comme question mais je ne vois pas XD
Cependant pour p>1 c'était facile
Modifié en dernier par
Irrot le 03 Mar 2017, 20:23, modifié 1 fois.
-
LjjMaths
- Membre Relatif
- Messages: 122
- Enregistré le: 26 Déc 2016, 00:46
-
 par LjjMaths » 03 Mar 2017, 20:06
par LjjMaths » 03 Mar 2017, 20:06
Salut, je ne comprends pas bien toutes ces notations mais tu peux également montrer l inégalité de Hodler commr ca :
On montre que pour tout

appartenant à R+,

par une étude de fonction
Ensuite on montre que

par récurrence
Puis, de ces 2 lemmes on déduit que

Et la c'est gagné car tu peux poser
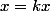
et

Et en trouvant un

adéquat tu obtient l inégalité
Il y a sûrement bcp plus simple mais bon

-
Irrot
- Membre Naturel
- Messages: 15
- Enregistré le: 25 Fév 2017, 18:08
-
 par Irrot » 03 Mar 2017, 20:11
par Irrot » 03 Mar 2017, 20:11
oui, cette partie la de la démo ne me pose pas de soucis ( c ce que j'ai utilisé pour p>1) mais en fait l'argument du corrigé ne fini pas de me convaincre. Quel notation pose soucis? les bra-kets c'est pour le produit scalaire. et les double barres pour la norme.
enfin pour moi c'est comme s'il était entrain de dire:
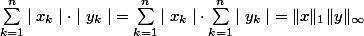
ce qui si j'ai bien compris est complètement faux

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Mar 2017, 20:28
par Ben314 » 03 Mar 2017, 20:28
Salut,
Irrot a écrit: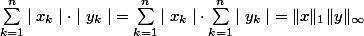
Faudrait peut être lire correctement le bidule : la norme sur x, c'est certes la norme 1, mais celle sur y, c'est la norme infinie.
Et, comme (par définition), on a

pour tout k, c'est que
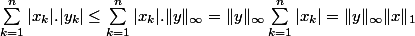
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Irrot
- Membre Naturel
- Messages: 15
- Enregistré le: 25 Fév 2017, 18:08
-
 par Irrot » 03 Mar 2017, 23:02
par Irrot » 03 Mar 2017, 23:02
Ben314 a écrit:
Merci bcp! je ne savais pas ça (enfin oui et non ) du coup c'est tout bon merci de ton aide

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Mar 2017, 23:14
par Ben314 » 03 Mar 2017, 23:14
Irrot a écrit:
Irrot a écrit: Ben314 a écrit:
. . . je ne savais pas ça (enfin oui et non ) . . .
??????????
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
