Inégalité a démontrer
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
andalous
- Membre Naturel
- Messages: 83
- Enregistré le: 15 Oct 2005, 15:10
-
 par andalous » 20 Sep 2006, 21:05
par andalous » 20 Sep 2006, 21:05
bonjour tout le monde voici mon exo
Prouver que pour tout réel t de ] 0 ; 1 [ il existe un unique Ot de ] 0 ; 1 [ tel que
ln( (1-t) / (1+t) ) = -2t / (1- t²(Ot)²)
En déduire linégalité suivante, valable pour t positif :
(exp2t)(1-t)/(1+t) < (ou egal) 1
il me semble que je suis mal parti car j'ai dérivé ln( (1-t) / (1+t) ) + 2t / (1- t²(Ot)²) mais je n'arrive pas à conclure pour le signe de la dérivé. A mon avis il doit y avoir une autre technique si vous pouvez m'aider merci
-
andalous
- Membre Naturel
- Messages: 83
- Enregistré le: 15 Oct 2005, 15:10
-
 par andalous » 21 Sep 2006, 16:13
par andalous » 21 Sep 2006, 16:13
salut personne ne peut m'aider, on m'a parlé d'un théoreme des accroissements finis mais on ne l'a pas encore apris donc je ne pense pas que je dois faire cela
-
abel
- Membre Relatif
- Messages: 258
- Enregistré le: 17 Mar 2006, 17:59
-
 par abel » 21 Sep 2006, 16:34
par abel » 21 Sep 2006, 16:34
Tu voulais pas remplacer tous les t par Ot dans ton égalité ?
Sinon on isole Ot et on l'exprime en fonction de t vu qu'il est censé dépendre de t.
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 22 Sep 2006, 19:45
par Aspx » 22 Sep 2006, 19:45
Chaud. J'ai du mal à voir apparaitre la manière de sortir le Ot. Ca donne des trucs trop foireux et vu qu'on est amené à dériver j'imagine ça va pas être très commode.
Genre :
}})
-
andalous
- Membre Naturel
- Messages: 83
- Enregistré le: 15 Oct 2005, 15:10
-
 par andalous » 22 Sep 2006, 21:50
par andalous » 22 Sep 2006, 21:50
oui je trouve pareil. j'ai essayé de dérivée (Ot)² je trouve un truk ou il est impossible de conclure qur le signe si vous pouvez m'aider merci
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Sep 2006, 23:17
par tize » 22 Sep 2006, 23:17
Ba c'est super, l'unicité vient de la formule et il ne reste plus qu'à démontrer que :
)
en changeant le sens de l'inégalité puisque
<0)
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 23 Sep 2006, 10:34
par Aspx » 23 Sep 2006, 10:34
Oui en gros le piège c'est qu'il faut utiliser argth. Je rappelle que :
 = \frac{1}{2}.\ln\(\frac{1+x}{1-x}\) \\<br />\Large \forall x \in ]-1;1[ , argth'(x) = \frac{1}{1-x^2}\)
Avec l'aide de tize et ce petit changement ça devrait plus t'aider :we:
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 23 Sep 2006, 11:34
par Aspx » 23 Sep 2006, 11:34
Par contre je ne comprends vraiment mais vraiment pas à quoi ça sert de montrer ça pour la question deux. Le résultat est assez immédiat en dérivant :
Soit
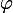
telle que
 = \e(2t).\frac{1-t}{1+t})
Alors
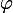
est dérivable et

on a :
 = \e(2t).(\frac{1-t}{1+t}+\frac{-(1+t)-(1-t)}{(1+t)^2}))
 = -\e(2t).\frac{t^2+1}{(1+t)^2} < 0)
Donc
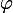
est décroissante or
 = 1)
et
 = -\infty)
Le problême est réglé et
 \leq 1)
:soupir2:
-
andalous
- Membre Naturel
- Messages: 83
- Enregistré le: 15 Oct 2005, 15:10
-
 par andalous » 23 Sep 2006, 17:53
par andalous » 23 Sep 2006, 17:53
merci tize et aspx mais je n'ai pas compris pourquoi l'unicité de Ot est dans la formule ??
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 23 Sep 2006, 18:19
par Aspx » 23 Sep 2006, 18:19
Il y a unicité de l'écriture car quand tu arrives à
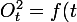)
tu es amené à prendre la racine et là il y a deux Ot qui vérifient cela. Un
positif, l'autre
négatif.
On met de côté celui qui est
négatif, donc il existe un
unique Ot
positif qui vérifie l'égalité de départ.
Ensuite on va
prouver qu'il est particulièrement dans ]0;1[
J'espère avoir été clair :euh:
-
andalous
- Membre Naturel
- Messages: 83
- Enregistré le: 15 Oct 2005, 15:10
-
 par andalous » 23 Sep 2006, 18:38
par andalous » 23 Sep 2006, 18:38
oui tres clair merci!
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 23 Sep 2006, 18:50
par Aspx » 23 Sep 2006, 18:50
Et tu es arrivé sinon pour après ? Montrer que c'est dans ]0;1[ ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
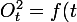) tu es amené à prendre la racine et là il y a deux Ot qui vérifient cela. Un positif, l'autre négatif.
tu es amené à prendre la racine et là il y a deux Ot qui vérifient cela. Un positif, l'autre négatif.