Images et noyau d'une application linéaire

[Dante0]

Bonjour,

J'aimerais avoir de l'aide sur cet exo : je dois trouver l'image et le noyau des application suivantes :

avec
M_1 =
\begin{pmatrix}
1 & -2 & 1 \\
-1 & 1 & 1 \\
2 & 1 & -1

\end{matrix}

M_2 = \begin{pmatrix}
1 & -2 & 1 \\
-1 & 1 & 0 \\
0 & -3 & 3

\end{matrix}

M_3 = \begin{pmatrix}
1 & -2 & 0 \\
2 & 1 & 1

\end{matrix}

M_4 =
\begin{pmatrix}
-1 & 0 \\
-1 & 3
2 & 1

\end{matrix}

Pourquoi le Latex de marche pas pour les matrices ? :hum:

[Yggdrasyll]

l'image est vect(C1,C2,C3) si (C1,C2,C3) n'est pas lié sinon tu dégages les vecteur en trop
et le noyau KerA il faut calculer AX=0 ou X est le vecteur colone (x,y,z)
ce qui donne un système

[Yggdrasyll]

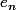
pour l'image ça revient à faire ou est un vecteur de la base canonique

[Dante0]

Je comprends pas trop pour l'image, je suis censé le trouver comment ?
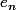
Ca ferait : ?

[sylvainc2]

Pour déterminer une base de l'image d'une matrice, c'est toujours la même chose: on fait le pivot de Gauss sur les vecteurs colonnes. Ceux, qui à la fin, ne sont pas à zéro sont indépendants donc ils forment une base de l'image.

Pour le noyau il faut résoudre Mx = 0, et ici aussi on peut utiliser le pivot de Gauss.

[Dante0]

Je comprends pas le concept, ca revient à faire quoi trouver l'image d'une application linéaire ?
Y'a moyen d'utiliser le latex ? Ca simplifierait la tâche des lecteurs. Il ne marche pas même si je ne pense pas m'être trompé... :/

[Kikoo <3 Bieber]

En effet, le TeX a un peu de mal avec les matrices. J'ai eu quelques problèmes aussi l'autre jour et ai du passer par un éditeur externe.
Je m'en vais notifier ce problème à Tom :)

[Dante0]

Pour déterminer une base de l'image d'une matrice, c'est toujours la même chose: on fait le pivot de Gauss sur les vecteurs colonnes. Ceux, qui à la fin, ne sont pas à zéro sont indépendants donc ils forment une base de l'image.

Pour le noyau il faut résoudre Mx = 0, et ici aussi on peut utiliser le pivot de Gauss.

Qu'est-ce que tu veux dire par "ceux qui ne sont pas à zéro" ?

[sylvainc2]

Le pivot de Gauss est un algo qui fait des combinaisons linéaires de vecteurs. L'image d'une matrice, c'est l'ensemble de toutes les combinaisons linéaires des vecteurs colonnes de la matrice. Donc en faisant le pivot sur les colonnes on va avoir une base de l'image de la matrice.

Je vais faire comme exemple le pivot de Gauss sur les colonnes de M1 :

1 -2 1
-1 1 1
2 1 -1

Le 1er pivot est 1, on fait donc : (C1,C2,C3 sont les colonnes de 1,2,3 de M1)

C2 = C2 – (-2/1)C1
C3 = C3 – (1/1)C1

Le résultat est :

1 0 0
-1 -1 2
2 5 -3

Le 2e pivot est -1, on fait:
C3 = C3 - (2/-1)C2

Résultat:

1 0 0
-1 -1 0
2 5 7

On voit qu'aucune des colonnes est (0,0,0) ca veut dire que tous les vecteurs colonnes sont linéairement indépendants. Pour une base de Im(M1) on peut prendre les colonnes de M1 correspondant aux colonnes qui ne sont pas nulles à la fin, dans ce cas-ci ce sont les 3 colonnes. Donc Im(M1) = R^3.

Quelques fois on n'est pas obligé de faire le pivot de Gauss quand c'est évident. Par exemple, Im(M3) est un sev de R^2 (car les vecteurs colonnes ont 2 composantes), et on voit bien que les colonnes 1 et 3 sont indépendantes, donc im(M3)={(1,2), (0,1)} par exemple.

[Dante0]

Je comprends pas du tout ta manière d'appliquer le pivot.. ca veut dire quoi le 1er pivot est 1, le 2e pivot est -1 ?
Normalement quand t'écris : C3 = C3 - (2/-1)C2 ca revient a dire C3 = C3 +2C2
Ca doit donner
0 3 1 non ? Je ne vois pas comment tu obtiens 2 5 7

En fait l'image d'une application linéaire représentée par une matrice va être les (ou la ?) colonne(s) de cette matrice qui (est) sont indépendante(s) ?

[Dante0]

Up :hein: :hein:

[Dante0]

Help svp :triste:

[sylvainc2]

Je comprends pas du tout ta manière d'appliquer le pivot.. ca veut dire quoi le 1er pivot est 1, le 2e pivot est -1 ?

Les pivots sont les éléments sur la diagonale. Au début le 1er pivot est l'élément ligne=1,colonne=1 de M1, c'est 1. Le 2e pivot est l'élément ligne 2 colonne 2 de la matrice du premier "résultat" soit -1. Le 3e pivot serait l'élément ligne 3 colonne 3 de deuxième résultat, soit 7, mais on n'en pas besoin puisque le calcul est terminé à ce moment-là.

Normalement quand t'écris : C3 = C3 - (2/-1)C2 ca revient a dire C3 = C3 +2C2
Ca doit donner
0 3 1 non ? Je ne vois pas comment tu obtiens 2 5 7

C1,C2,C3 c'est pour colonne 1,2,3 pas ligne. On fait le pivot de gauss sur les colonnes. Si tu insistes pour le faire sur les lignes, transpose M1 au début puis fait-le sur les lignes. Ca revient au même.

En fait l'image d'une application linéaire représentée par une matrice va être les (ou la ?) colonne(s) de cette matrice qui (est) sont indépendante(s) ?

Oui c'est ca.

[Dante0]

Les pivots sont les éléments sur la diagonale. Au début le 1er pivot est l'élément ligne=1,colonne=1 de M1, c'est 1. Le 2e pivot est l'élément ligne 2 colonne 2 de la matrice du premier "résultat" soit -1. Le 3e pivot serait l'élément ligne 3 colonne 3 de deuxième résultat, soit 7, mais on n'en pas besoin puisque le calcul est terminé à ce moment-là.

Mais c'est curieux... pour moi le pivot ca va par exemple être une ligne de la matrice (si on applique le pivot de gauss sur les lignes) par exemple L1 c'est a dire la ligne qu'on va garder fixe... Je saisis pas du tout l'histoire de la diagonale, je sais pas si ca revient au même mais c'est pas du tout comme ca qu'on m'a appris le pivot de gauss... :/

[Dante0]

Pour M1 dans la correction on dit que :
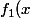car étant surjective, Imf est l'espace d'arrivée de
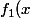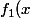Est-ce que le nombre de lignes ou de colonnes importe ici pour l'image ? Est-ce qu'on aurait pu par exemple dire que car étant injective, Imf est l'espace de départ de ?

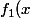Pour la matrice M2 son rang est de 2 mais elle n'est ni injective ni surjective que peut-on conclure sur son image ?

[Dante0]

up :hein: :hein:

[Dante0]

Up ! :we: :we: