Noyau d'une application linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Déc 2013, 17:29
par barbu23 » 13 Déc 2013, 17:29
Bonjour à tous, :happy3:
S'il vous plaît, quel est le noyau de l'application linéaire
 / F_1 $)
?
Et est ce que le théorème de factorisation s'applique dans ce cas là ?
Merci d'avance. :happy3:
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 13 Déc 2013, 17:33
par arnaud32 » 13 Déc 2013, 17:33
 = 0)
ca veut dire quoi?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Déc 2013, 17:40
par barbu23 » 13 Déc 2013, 17:40
arnaud32 a écrit: = 0)
ca veut dire quoi?
désolé, j'ai corrigé le premier message. :happy3:
 = 0 \ \ \Longleftrightarrow \ \ y \in F_1 $)
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 13 Déc 2013, 17:41
par arnaud32 » 13 Déc 2013, 17:41
barbu23 a écrit:désolé, j'ai corrigé le premier message. :happy3:
 = 0 \ \ \Longleftrightarrow \ \ y \in F_1 $)
donc
=0)
veut dire ...
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Déc 2013, 17:54
par barbu23 » 13 Déc 2013, 17:54
arnaud32 a écrit:donc
=0)
veut dire ...
 = 0 \ \ \Longleftrightarrow \ \ f(x) \in F_1 \bigcap \mathrm{Im} f = \{ 0 \} $)
Donc :
 = 0 $)
, c'est à dire

Par conséquent
 \subset \mathrm{ker} f $)
.
Qu'est ce qu'on fait ensuite. On montre que :
 $)
?
Merci d'avance. :happy3:
Edit : Soit

, alors
 = 0 $)
, c'est à dire
) = \pi ( 0 ) = \overline{0} $)
, par conséquent :
 $)
?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Déc 2013, 18:54
par barbu23 » 13 Déc 2013, 18:54
svp, est ce que l'application

est surjectif quelque soit

?
Merci d'avance. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Déc 2013, 18:57
par Ben314 » 13 Déc 2013, 18:57
barbu23 a écrit:svp, est ce que l'application

est surjectif quelque soit

?
Merci d'avance. :happy3:
oui. Elle l'est par construction.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Déc 2013, 19:00
par barbu23 » 13 Déc 2013, 19:00
Merci beaucoup @Ben314. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Déc 2013, 19:04
par Ben314 » 13 Déc 2013, 19:04
De toute façon, il faut bien voir que, quasi par construction, la projection cannonique
 / F_2)
induit un isomorphisme de
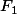
sur
 / F_2)
(dans le cadre des espaces vectoriels)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Déc 2013, 19:16
par barbu23 » 13 Déc 2013, 19:16
D'accord, merci beaucoup @Ben314. :lol3:
Soit
 / F_1 $)
avec

:
Alors

et

Par conséquent

.
Donc

tel que
 = y $)
Par conséquent
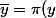 = \pi (f(x)) $)
D'où
 ) $)
est surjective.
Correct ?
Pourquoi

possède un antecedent par

?
Merci d'avance.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 13 Déc 2013, 19:28
par barbu23 » 13 Déc 2013, 19:28
Ben314 a écrit:la projection cannonique
 / F_2)
induit un isomorphisme de
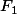
sur
 / F_2)
(dans le cadre des espaces vectoriels)
Donc,

devient

qui est une surjection, je pense, mais, je ne sais pas pourquoi. :happy3:
Merci d'avance pour vos éclaircissements. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Déc 2013, 22:00
par Ben314 » 13 Déc 2013, 22:00
barbu23 a écrit:Soit
 / F_1 $)
avec

:
Alors

et

Par conséquent

.
Là, ça déconne : ce n'est pas parce qu'un élément de la somme n'est pas dans un des termes qu'il est forcément dans l'autre vu que la somme de deux s.e.v. est bien plus "grosse" que la réunion des deux s.e.v.
Si tu prend un
 / F_1)
(nul ou pas, ça ne change rien), et que tu écrit
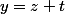
avec

et

alors
=\{z+s\text{ avec } s\in F_1\})
dont l'intersection avec

est réduite au singleton

.
Cela montre que la restriction de

à

est bijective.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
avec
:
et
.