Image d une application lineaire

[anna747]

Bonjour


J aimerais avoir votre aide pour enfin comprendre des choses en algebre lineaire ou je suis completement paumee



J ai la matrice suivante: A= -1 1 0
-3 -2 -3
-3 -2 -3

J ai im (f)=Vect(( 1, -1,-1),(1,-3,-3))

Comment trouver le plan d equation de l image?

[mathelot]

Bonjour


J aimerais avoir votre aide pour enfin comprendre des choses en algebre lineaire ou je suis completement paumee



J ai la matrice suivante: A= -1 1 0
-3 -2 -3
-3 -2 -3

J ai im (f)=Vect(( 1, -1,-1),(1,-3,-3))

Comment trouver le plan d equation de l image?

bonjour ,
au niveau des dimensions, on a toujours
(1) où E=R_3 espace de départ

Une méthode possible est de se servir des coordonnées (x;y;z) comme scalaires
dans des combinaisons linéaires de vecteurs de base.
pour caractériser le noyau



ssi



ssi



ssi



le noyau est donc une droite vectorielle, de vecteur de base


d'après (1), l'image est donc un sous espace de dimension 2, ie, un plan vectoriel.

[mathelot]

ssi







ssi




que l'on écrit



on a donc exhibé une famille génératice de Im(f)
composée de trois vecteurs non linéairement indépendants.
Le troisième vecteurs est combinaison linéaire des deux précédents.


pour déterminer que
dim(Im(f))=2,
il s'agit de montrer que le rang de
est 2, à l'aide de la théorie des déterminants.

[mathelot]

étude du rang de f






L'image est de dimension 2,ie, le rang de f est 2.

remarque: le rang d'une famille finie de vecteurs est:
- la dimension du sous espace qu'elle engendre
- le nombre maximal de vecteurs formant une famille libre
- la taille du plus grand déterminant mineur non nul

[mathelot]

Pour le cours ,tu peux consulter

"algèbre linéaire" de J.Grifone chez Cépaduès Edition
et
"exercices d'algèbre linéaire et bilinéaire" de J-B Hiriart chez le même éditeur.

Bonne journée.

[anna747]

Merci Mathelot pour ton aide. Je te remercie infiniment.

En revanche pour l equation du plan de l image, le prof a affirme dans la correction du Td non detaillee que IM f est le plan d equation y=z .

Je ne comprends pas bien evidemment pas, je pense que c est tellement simple que le prof n a pas pense a detailler mais moi je suis perdue.

Merci encore Mathelot.

[mathelot]

je fais la liaison entre ce que t'a dit ton prof (vrai) et mes résultats (vrais également)

1)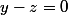 est l'équation d'un plan vectoriel
car , en dimension 3, les plans vectoriels ont pour équation

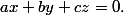
ce sont des noyaux de forme linéaire.

à partir de la dimension quatre, on les nomme "hyperplans".

2)
soit

donc



mais est de dimension 2 car f est de rang 2.

dc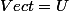

d'après
propriétés: si trois vecteurs appartiennent à un sous-espace V
V contient leurs combinaisons linéaires (qui est également un sous-espace vectoriel)

Si un plan vectoriel P1 contient une famille génératrice de vecteurs d'un plan vectoriel P2
alors P1=P2

résultat des courses est une base de U.

[zygomatique]

Bonjour


J aimerais avoir votre aide pour enfin comprendre des choses en algebre lineaire ou je suis completement paumee



J ai la matrice suivante: A= -1 1 0
-3 -2 -3
-3 -2 -3

J ai im (f)=Vect(( 1, -1,-1),(1,-3,-3))

Comment trouver le plan d equation de l image?

salut

comme tu le vois u = (1, -1, -1) et v = (1, -3, -3) vérifient y = z

A(x, y, z) = (-x + y, -3x - 2y - 3z, -3x - 2y - 3z) = (X, Y, Z)

il est donc évident que Im(f) est le plan d'équation Y = Z

:lol3:

[mathelot]

désigne l'ensemble des combinaisons linéaires
de f1,f2,f3. C'est un sous espace vectoriel de et de .

[anna747]

désigne l'ensemble des combinaisons linéaires
de f1,f2,f3. C'est un sous espace vectoriel de et de .

Merci Mathelot et Zygomatique d avoir pris le temps de me repondre. Si vous etes prof de mathematiques, je souhaiterais vivement vous echanger contre le mien.

Encore un grand merci votre explication m a beaucoup aidee. reste a voir maintenant si je saurai le mettre en pratique dans un autre exercice.