Image Imf d'une application linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Déc 2012, 14:55
par Dante0 » 02 Déc 2012, 14:55
Bonjour,
Quelqu'un pourrait m'expliquer comment trouver l'mage d'une application linéaire ?
Dans certains bouquins je trouve
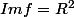
donc je ne sais pas trop ce que c'est, un nombre, une dimension, un espace... ?
Merci !
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 02 Déc 2012, 15:03
par cuati » 02 Déc 2012, 15:03
Dante0 a écrit:Bonjour,
Quelqu'un pourrait m'expliquer comment trouver l'mage d'une application linéaire ?
Dans certains bouquins je trouve
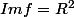
donc je ne sais pas trop ce que c'est, un nombre, une dimension, un espace... ?
Merci !
Bonjour,
si
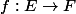
est une application linéaire entre deux espaces vectoriels alors
=\{f(x) ; x\in E\})
et c'est un sous espace vectoriel de

.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Déc 2012, 15:13
par Dante0 » 02 Déc 2012, 15:13
cuati a écrit:Bonjour,
si
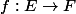
est une application linéaire entre deux espaces vectoriels alors
=\{f(x) ; x\in E\})
et
c'est un sous espace vectoriel de 
.
Est-ce toujours le cas ?
Voila ce que j'ai marqué dans mon cours :
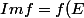 = \{AX ; X\in E\})
L'ensemble Imf est donc engendré par les colonnes de A, qui sont les images par f(.) des vecteurs de la base canonique de l'espace de départ de f(.). Ces colonnes étant des éléments de F, Imf est un sous-espace vectoriel de F. Comme il est engendré par les colonnes de A on a :
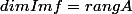
J'ai du mal à comprendre la première partie jusqu'a "ces colonnes étant des éléments de F"
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 02 Déc 2012, 16:09
par cuati » 02 Déc 2012, 16:09
Dante0 a écrit:Est-ce toujours le cas ?
Voila ce que j'ai marqué dans mon cours :
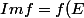 = \{AX ; X\in E\})
L'ensemble Imf est donc engendré par les colonnes de A, qui sont les images par f(.) des vecteurs de la base canonique de l'espace de départ de f(.). Ces colonnes étant des éléments de F, Imf est un sous-espace vectoriel de F. Comme il est engendré par les colonnes de A on a :
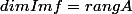
J'ai du mal à comprendre la première partie jusqu'a "ces colonnes étant des éléments de F"
Le mélange application linéaire/représentation matricielle ne me semble pas des plus judicieux...
bref, le passage en question dit que l'image des vecteurs de la base canonique sont les vecteurs colonnes de la matrice A. En gros si e1=(1,0,0,...,0) alors Ae1=C1, où C1 est la première colonne de A (même chose avec i à la place de 1). Comme tout vecteur de E s'écrit comme combinaison linéaire de vecteurs (ei) on remarque alors, avec ce que l'on a dit précédemment, que tout vecteur de Im(f) s'écrit comme combinaison linéaire des vecteurs colonnes de la matrice A.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Déc 2012, 16:20
par Dante0 » 02 Déc 2012, 16:20
Okay !
Du coup si je veux trouver Imf de la matrice suivante :
3 4 2
1 1 0
5 3 2
Je m'y prends comment ?
PS: rien a voir mais comment interpréter kerf = {0} ? (lorsque l'application est injective)
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 02 Déc 2012, 17:26
par cuati » 02 Déc 2012, 17:26
Dante0 a écrit:Okay !
Du coup si je veux trouver Imf de la matrice suivante :
3 4 2
1 1 0
5 3 2
Je m'y prends comment ?
PS: rien a voir mais comment interpréter kerf = {0} ? (lorsque l'application est injective)
Bon de manière simple et sans réfléchir l'image dans ce cas là est l'ensemble des combinaisons linéaire des vecteurs colonnes :
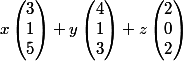
pour tout x,y,z.
Mais ça c'est trop facile comme réponse... comme tu l'as écrit dim (Im (f))=rg(A). Montre que le rang de A est égal à 3, ainsi Im(f) est un sous espace vectoriel de

de rang 3 donc
=\mathbb{R}^3)
.
Pour ta seconde question, Ker(f)={0} signifie que seul le vecteur nul a une image nul. Pour une application linéaire cela revient à dire qu'elle est injective. Il y a un théorème classique mais capital qui relie Ker(f) avec Im(f), c'est le théorème du rang (que tu as sans doute déjà vu en cours)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Déc 2012, 17:31
par Dante0 » 02 Déc 2012, 17:31
cuati a écrit:Bon de manière simple et sans réfléchir l'image dans ce cas là est l'ensemble des combinaisons linéaire des vecteurs colonnes :
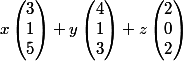
pour tout x,y,z.
Mais ça c'est trop facile comme réponse...
comme tu l'as écrit dim (Im (f))=rg(A). Montre que le rang de A est égal à 3, ainsi Im(f) est un sous espace vectoriel de  de rang 3 donc
de rang 3 donc =\mathbb{R}^3)
.
Pour ta seconde question, Ker(f)={0} signifie que seul le vecteur nul a une image nul. Pour une application linéaire cela revient à dire qu'elle est injective. Il y a un théorème classique mais capital qui relie Ker(f) avec Im(f), c'est le théorème du rang (que tu as sans doute déjà vu en cours)
Pourquoi une combinaison linéaire en fait ??
Trouver l'image ca revient pas à trouver les x y z ?
Sinon je comprends pas comment tu as fait avec la phrase en gras.. pourquoi imf serait un SEV de R3 et pourquoi ca impliquerait que Imf = R3 ?
Je connais le théorème des dimensions pas du rang, c'est quoi en fait ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 02 Déc 2012, 17:44
par cuati » 02 Déc 2012, 17:44
Dante0 a écrit:Pourquoi une combinaison linéaire en fait ??
Trouver l'image ca revient pas à trouver les x y z ?
Sinon je comprends pas comment tu as fait avec la phrase en gras.. pourquoi imf serait un SEV de R3 et pourquoi ca impliquerait que Imf = R3 ?
Je connais le théorème des dimensions pas du rang, c'est quoi en fait ?
Bon...
Im(f) est un sous espace vectoriel de R3, on ne cherche donc pas x,y et z ! Mais tous les vecteurs de R3 qui peuvent appartenir à Im(f). Par définition un vecteur

appartient à Im(f) si et seulement si il existe un autre vecteur
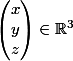
tel que
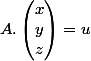
.
Quand on multiplie A avec
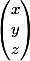
on obtient justement ce que je t'ai écrit dans mon message précédent. C'est juste une manière de décrire tous les vecteurs possibles qui sont dans Im(f), tu peux choisir n'importe quels nombres à la place de x,y et z tu auras alors un vecteur de Im(f).
Sinon f est une application linéaire à valeur dans R3, Im(f) est donc un sous espace vectoriel de R3 (il suffit de l'écrire pour s'en rendre compte). Je te rappelle que R3 est de dimension 3. Si tu montres que rang(f)=Dim(Im(f))=3 alors tu montres que Im(f) est un sous espace vectoriel de dimension 3 dans R3 (lui même de dimension 3)... on a donc pas vraiment le choix Im(f)=R3.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Déc 2012, 18:39
par Dante0 » 02 Déc 2012, 18:39
cuati a écrit:Bon...
Im(f) est un sous espace vectoriel de R3, on ne cherche donc pas x,y et z ! Mais tous les vecteurs de R3 qui peuvent appartenir à Im(f). Par définition un vecteur

appartient à Im(f) si et seulement si il existe un autre vecteur
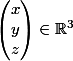
tel que
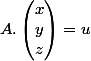
.
Quand on multiplie A avec
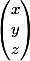
on obtient justement ce que je t'ai écrit dans mon message précédent. C'est juste une manière de décrire tous les vecteurs possibles qui sont dans Im(f),
tu peux choisir n'importe quels nombres à la place de x,y et z tu auras alors un vecteur de Im(f).Sinon f est une application linéaire à valeur dans R3, Im(f) est donc un sous espace vectoriel de R3 (il suffit de l'écrire pour s'en rendre compte). Je te rappelle que R3 est de dimension 3. Si tu montres que rang(f)=Dim(Im(f))=3 alors tu montres que Im(f) est un sous espace vectoriel de dimension 3 dans R3 (lui même de dimension 3)... on a donc pas vraiment le choix Im(f)=R3.
En fait Imf c'est jamais un ensemble de vecteurs précis ? Il doit toujours être caractérisé par un ensemble général (R2, R3, R4 etc...) ?
Est-ce que c'est possible par exemple de trouver que Imf = (1,2) en colonne par exemple ?
Sinon si on prend un autre exemple :
1 -2 1
-1 1 0
0 -3 3
Le rang de cette matrice est 2 comme on sait que rangA = rang f = dimImf = 2
Qu'est-ce qu'on peut en conclure sur Imf ?
La réponse c'est : Imf est le sous espace vectoriel de R3 engendré par les colonnes de A... Je comprends pas trop. :/
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 02 Déc 2012, 19:26
par cuati » 02 Déc 2012, 19:26
Dante0 a écrit:En fait Imf c'est jamais un ensemble de vecteurs précis ? Il doit toujours être caractérisé par un ensemble général (R2, R3, R4 etc...) ?
Est-ce que c'est possible par exemple de trouver que Imf = (1,2) en colonne par exemple ?
Sinon si on prend un autre exemple :
1 -2 1
-1 1 0
0 -3 3
Le rang de cette matrice est 2 comme on sait que rangA = rang f = dimImf = 2
Qu'est-ce qu'on peut en conclure sur Imf ?
La réponse c'est : Imf est le sous espace vectoriel de R3 engendré par les colonnes de A... Je comprends pas trop. :/
Si, Im(f) est un ensemble de vecteurs précis puisque c'est un sous espace vectoriel, mais c'est pas toujours R, R2, R3, dans R2 cela peut être un sous espace vectoriel de dimension 1 (une droite autrement dit).
Il n'est pas possible de trouver Imf = (1,2) car le vecteur (1,2) n'est pas un espace vectoriel !
Pour ton autre exemple, on en déduit que Im(f) est un espace vectoriel de dimension 2 (un plan vectoriel autrement dit). Avec peu de calcul on peut même montrer qu'il est engendré par les vecteurs
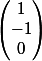
et
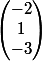
puisque le 3ème vecteur colonne s'obtient comme étant l'opposé de la somme des deux premiers...
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Déc 2012, 19:37
par Dante0 » 02 Déc 2012, 19:37
Donc Imf = R^2 dans ce cas ? Ils se seraient trompés dans la correction ?
Je pense avoir compris quelque chose pour ca je vais prendre 2 autres exemple :
1 -2 0
-2 1 1
Est-ce que la notion d'image a qqc a voir avec le fait que la matrice soit injective ou surjective ? Parce que dans ce cas la réponse c'est : imf = R^2 car la matrice étant surjective Imf est l'espace d'arrivée de cette matrice (=nombre de ligne donc 2)
2e exemple :
-1 0
-1 3
2 1
Réponse : Imf est le sous espace vectoriel de R3 engendré par les colonne de cette matrice.
Pourtant puisqu'elle est injective moi j'aurais dit que Imf = R^2 car la matrice étant injective Imf est l'espace de départ de cette matrice ()nombre de colonne donc 2) pourquoi ce n'est pas le cas ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 02 Déc 2012, 20:13
par cuati » 02 Déc 2012, 20:13
Dante0 a écrit:Donc Imf = R^2 dans ce cas ? Ils se seraient trompés dans la correction ?
Je pense avoir compris quelque chose pour ca je vais prendre 2 autres exemple :
1 -2 0
-2 1 1
Est-ce que la notion d'image a qqc a voir avec le fait que la matrice soit injective ou surjective ? Parce que dans ce cas la réponse c'est : imf = R^2 car la matrice étant surjective Imf est l'espace d'arrivée de cette matrice (=nombre de ligne donc 2)
2e exemple :
-1 0
-1 3
2 1
Réponse : Imf est le sous espace vectoriel de R3 engendré par les colonne de cette matrice.
Pourtant puisqu'elle est injective moi j'aurais dit que Imf = R^2 car la matrice étant injective Imf est l'espace de départ de cette matrice ()nombre de colonne donc 2) pourquoi ce n'est pas le cas ?
NON ! Im(f) n'est pas égal à R^2, Im(f) est un sous espace de R^3 qui est de dimension 2 ! C'est donc un plan vectoriel (tu n'as qu'à imaginer un plan qui passe par l'origine dans l'espace...)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Déc 2012, 20:23
par Dante0 » 02 Déc 2012, 20:23
En fait j'arrive pas du tout à déterminer la méthode qui me permettent de trouver l'image. Lorsque je suis face à une matrice 3x3 qui représente une application linéaire par exemple par quoi je devrais commencer si je cherche à déterminer son image ?
-
Halloweed
- Membre Naturel
- Messages: 26
- Enregistré le: 10 Nov 2012, 21:51
-
 par Halloweed » 02 Déc 2012, 20:44
par Halloweed » 02 Déc 2012, 20:44
Dante0 a écrit:En fait j'arrive pas du tout à déterminer la méthode qui me permettent de trouver l'image. Lorsque je suis face à une matrice 3x3 qui représente une application linéaire par exemple par quoi je devrais commencer si je cherche à déterminer son image ?
Salut,
Ce n'est pas très compliqué, la méthode générale c'est:
*Tu calcule le rang de la matrice, ce qui te donne la dimension de son image (avec la pratique et/ou pour les matrices et applications simples c'est une étape qu'on peut sauter, mais si tu as un doute sur ton résultat ça peut être un bon moyen de vérification).
*Ensuite, si par exemple le rang est 2, tu cherches les deux vecteurs colonne de ta matrice qui sont libres (linéairement indépendants si tu préfères), notons v1 et v2.
*Im(A), A étant ta matrice, c'est donc Vect(v1,v2), ou l'espace vectoriel (plan vectoriel dans ce cas) engendré par les deux vecteurs.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Déc 2012, 21:20
par Dante0 » 02 Déc 2012, 21:20
Halloweed a écrit:Salut,
Ce n'est pas très compliqué, la méthode générale c'est:
*Tu calcule le rang de la matrice, ce qui te donne la dimension de son image (avec la pratique et/ou pour les matrices et applications simples c'est une étape qu'on peut sauter, mais si tu as un doute sur ton résultat ça peut être un bon moyen de vérification).
*Ensuite, si par exemple le rang est 2, tu cherches les deux vecteurs colonne de ta matrice qui sont libres (linéairement indépendants si tu préfères), notons v1 et v2.
*Im(A), A étant ta matrice, c'est donc Vect(v1,v2), ou l'espace vectoriel (plan vectoriel dans ce cas) engendré par les deux vecteurs.
Dans ce cas Im(A) c'est le nombre de vecteurs de A linéairement indépendants donc c'est le rang de A tout simplement ?
-
Halloweed
- Membre Naturel
- Messages: 26
- Enregistré le: 10 Nov 2012, 21:51
-
 par Halloweed » 02 Déc 2012, 23:19
par Halloweed » 02 Déc 2012, 23:19
Dante0 a écrit:Dans ce cas Im(A) c'est le nombre de vecteurs de A linéairement indépendants donc c'est le rang de A tout simplement ?
Non non le rang de A c'est la dimension de Im(A)
Im(A) c'est l'espace vectoriel (sous espace vectoriel pour être plus précis, de R^3 dans cet exemple) engendré par ces vecteurs libres.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Déc 2012, 23:50
par Dante0 » 02 Déc 2012, 23:50
Halloweed a écrit:Non non le rang de A c'est la dimension de Im(A)
Im(A) c'est l'espace vectoriel (sous espace vectoriel pour être plus précis, de R^3 dans cet exemple) engendré par ces vecteurs libres.
Mais mathématiquement ca se note comment ?
-
Halloweed
- Membre Naturel
- Messages: 26
- Enregistré le: 10 Nov 2012, 21:51
-
 par Halloweed » 03 Déc 2012, 20:47
par Halloweed » 03 Déc 2012, 20:47
Dante0 a écrit:Mais mathématiquement ca se note comment ?
Ben ça se note Vect(v1,v2,....,vn) les vn étant tes vecteurs libres..
-
marina10
- Messages: 1
- Enregistré le: 20 Mai 2014, 18:33
-
 par marina10 » 20 Mai 2014, 18:45
par marina10 » 20 Mai 2014, 18:45
bnsr aidez moi svp dans cet exercice , on f: R3 ;)R2 une application :f(x,y,z)= (-x+y+z, x-y+z).
1- vérifier si elle est R-linéaire?
2- donner une base de KERF en déduire sa dimension?
3- donner une base de Imf en déduire sa dimension?
4- donner la matrice A de f relativement à la base canonique de R3 et R2 ? merci d'avance
-
Anaisdeistres
- Membre Relatif
- Messages: 175
- Enregistré le: 29 Oct 2018, 19:37
-
 par Anaisdeistres » 19 Nov 2018, 21:34
par Anaisdeistres » 19 Nov 2018, 21:34
1) f(x+x',y+y',z+z')= (-x-x'+y+y'+z+z', x+x'-y-y'+z+z')
On prend λ ∈ R,
λf(x+x',y+y',z+z')= (λ(-x+y+z), λ(x-y+z))
Donc f linéaire.
2) On cherche une base de Ker f
[L1] -x+y+z=0 équivalent à x=z+y
[L2] x-y+z=0
[L1+L2] z=0
[L1]x=y
x quelconque
u=(1,1,0) non null et libre donc Vect(u) est une base de ker f de dim 1
3) Im f est de dim 2 et Vect((-1,1),(1,1)) est une base de Im f
4) On cherche une base canonique de R3
A=Vect((1,0,0),(0,1,0),(0,0,1))
On cherche une base canonique de R2
A=Vect((1,0),(0,1))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
donc je ne sais pas trop ce que c'est, un nombre, une dimension, un espace... ?
est une application linéaire entre deux espaces vectoriels alors
et c'est un sous espace vectoriel de
.
pour tout x,y,z.
de rang 3 donc
.
appartient à Im(f) si et seulement si il existe un autre vecteur
tel que
.
on obtient justement ce que je t'ai écrit dans mon message précédent. C'est juste une manière de décrire tous les vecteurs possibles qui sont dans Im(f), tu peux choisir n'importe quels nombres à la place de x,y et z tu auras alors un vecteur de Im(f).