Ensemble image d'une application linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 02 Oct 2005, 12:03
par Anonyme » 02 Oct 2005, 12:03
salut, une question peut-être triviale pour vous mais dont je ne suis pas sur.
soit n applications linéaires (f1, f2, ...fn) endormorphisme d'espaces vectoriels E.
at-on Im(f1+...+fn)=Im(f1)+Im(f2)+...+Im(fn)?
pour moi la réponse est évidemment oui.pour vous, c'est quoi?
-
phenomene
- Membre Relatif
- Messages: 313
- Enregistré le: 04 Aoû 2005, 07:09
-
 par phenomene » 02 Oct 2005, 12:19
par phenomene » 02 Oct 2005, 12:19
Bonjour, plutôt que de te baser sur un vague "évidemment", essaie de démontrer ton égalité... Il y a une inclusion en effet évidente, mais pour l'inclusion réciproque... je te laisse chercher.
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 02 Oct 2005, 12:23
par Galt » 02 Oct 2005, 12:23
Bonjour
La réponse est non, parce que, quand on fait

, on peut prendre n'importe quelle combinaison
+f_2(x_2)+...+f_n(x_n))
, tandis que dans
)
on a forcément
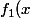+...+f_n(x))
avec le même x. Tu ne devrais pas avoir de mal à trouver un contre exemple
-
phenomene
- Membre Relatif
- Messages: 313
- Enregistré le: 04 Aoû 2005, 07:09
-
 par phenomene » 02 Oct 2005, 12:29
par phenomene » 02 Oct 2005, 12:29
Pour trouver un contre-exemple, on peut se limiter à

et

; ce n'est pas très difficile.
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 02 Oct 2005, 12:34
par Galt » 02 Oct 2005, 12:34
On peut même se limiter à

-
phenomene
- Membre Relatif
- Messages: 313
- Enregistré le: 04 Aoû 2005, 07:09
-
 par phenomene » 02 Oct 2005, 12:38
par phenomene » 02 Oct 2005, 12:38
Galt a écrit:On peut même se limiter à

Ah oui, je n'étais pas réveillé. :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
