Salut Night !
les angles de vecteurs sont les matrices de rotation

avec
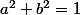
et

et
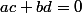
si tu souhaites toute la généralité , les coefficients sont dans un corps K
plus prudemment, dans R
maintenant dans R, la série
^k}{k!})
est un morphisme surjectif et en passant au quotient (le fameux modulo

) donne les différentes mesures d'un angle,
toutes dans la même classe
le grand mystère dans tout cela, c'est que cos() et sin(), les coordonnées
génériques du point du cercle,
sont limites uniformes, sur tout compact de R, comme partie réelle et imaginaire de l'exponentielle
d'une suite de polynômes bien particulière