Homéomorphisme

[MacManus]

Bonsoir

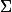
On considère la surface de d'équation :

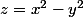
On pose : u=x-y et v=x+y

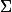
(1) écrire l'équation de dans les coordonnées (u,v,z)
==> z=uv
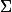
(2) en déduire un paramétrage de par (u,v)
==> , ,
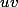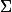
(3) montrer que est homéomorphe à
==> ??

je veux bien un peu d'aide svp. Merci bcp

[ToToR_2000]

Vu dans wikipedia:

En topologie, un homéomorphisme est une application bijective continue entre deux espaces topologiques dont la réciproque est continue.

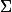
est une application de dans qui est continue (c'est assez clair) et qui est injective parce que phi(u1,v1) = phi(u2, v2) => (u1,v1) = (u2,v2) (à démontrer)
et surjective puisque si l'on prend (x,y,z) appartenant à la surface alors on peut trouver (u,v) tel que phi(u,v) = (x,y,z) (à démontrer aussi)
Donc c'est une bijection et elle admet donc un inverse qu'il faut calculer.
Et enfin il faut montrer que l'inverse est continu pour conclure.

[MacManus]

Ok merci beaucoup Totor, ça se fait bien !

[Ben314]

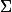
Par contre, je vois absolument pas l'intérêt de u et de v pour montrer que est homéomorphe à R² : on prendrait directement (x,y)->(x,y,x²-y²) que ça marcherais pareil (voir même mieux...)

[MacManus]

Moui c'est bien vrai ça !
et c'est même plus rapide...

Au fait, j'ai une autre question, est-ce que définie un plongement ? (plongement = continue + injective + ouverte(sur son image))

[MacManus]

je pense que oui puisque si je choisi un ouvert de la surface, alors son image par l'application réciproque de phi est un ouvert du plan (car phi est continue)... mais bon...je demande


Oui c'est vrai : homéomorphisme => ouverte

[Ben314]

Ben, déjà, ta définition de "plongement" me surprend un peu.
La seule déf. de "plongement" que je connais à peu prés est celle du cadre de la géométrie diff. et c'est pas tout à fait ça (on demande à f d'être un homéo sur son image et qu'en tout point la différentielle soit injective)

Tu est sûr de ton coup pour ta définition ?
(parce que, dans ce cas, je vois pas bien la différence avec une fonction qui est un homéo. sur son image...)

[MacManus]

c'est la déf que j'ai dans mon cours, mais bon je ne prétends pas avoir LA définition... en tout cas, ce que tu dis me fait penser à la définition d'une immersion (différentielle injective en tout point (mais alors par contre sans "homéo") ...

[Ben314]

Bon, résumons : soit f:E->F (espace topo)

1) Si f est un homéo de E sur f(E) alors f est continue, injective et ouverte sur son image

2) Si f est continue, injective et ouverte sur son image alors elle est bijective de E sur f(E), et sa bijection réciproque est continue vu que f est ouverte donc c'est un homéo sur son image...

[Ben314]

Bon, j'ai fini par aller vérifier sur Wiki (pour voir si je devenais gateux) :
Immersion : différentielle injective.
Plongement : homéomorphisme sur son image ET différentielle injective.

[MacManus]

Ok j'ai pris note, merci !

[Ben314]

Bon, aprés, en réfléchissant un peu, dans le cadre uniquement topologique (i.e. sans structures différentielles), ça parrait raisonable de définir un "plongement" comme une application qui réalise un homéomorphisme sur son image (ce qui, j'insiste..., me semble être la même chose qu'une application continue, injective et ouverte sur son image)

Bon, en résumé, je pense que ça dépend si ton cours, c'est plutôt "topologie" toute seule ou plitôt "calcul diff"...

[MacManus]

oui c'est plus du calcul diff.
mais bon merci pour toutes tes précisions, j'ai de tte façon noté tout ça, et j'ai compris l'idée.