Homéomorphisme de R dans R2

[Niki42]

Bonjour à tous ,
J’étudie la actuellement la connexité et une question (bête) me taraude malheureusement l’esprit et je viens la poser en toute humilité sur ce forum ^^

Revient souvent le fait que R ne soit pas homéomorphe à R2.
Mais si par exemple à tout x de R j’associe
x—> ( x, exp(x)) , ou x—> (1, exp(x)) ,je viens pas d’exhiber un homéomorphisme sur ces deux ensembles ?

Merci par avance !

[Mateo_13]

Bonjour,

en fait, tu as exhibé un homéomorphisme de sur son image, qui est une courbe incluse dans , mais pas tout entier.

Si une bijection non bi-continue entre ces deux ensembles t'intéresse, regarde la vidéo de Burkard Polster :
https://youtu.be/ZUHWNfqzPJ8

Cordialement,

[GaBuZoMeu]

Tu parles de connexité. Tu fais sans doute allusion au fait que n'est pas homéomorphe à 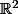parce que moins un point n'est pas connexe, tandis que 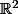moins un point est connexe ?

[Niki42]

Exact, la réponse de Mateo m’a éclairé !
Merci à tous les deux