Hölder Généralisé :

[Nightmare]

Hello,

Je vous propose de trouver toutes les fonctions de classe telles que :

- est une bijection strictement croissante de réciproque , et tend vers 0 en 0.

- Pour toutes fonctions continues :





L'inégalité de Hölder fournit les fonctions puissances. What else?

[Nightmare]

Pas d'idées? Autant vous le dire pour vous éviter de chercher des contres exemples trop alambiqués : seules les fonctions puissances conviennent. A prouver !

[windows7]

aucune pour l'instant, mais laisse nous( moi ? ) encore reflechir un peu

[ffpower]

J'ai pour l'instant obtenu que F et G étaient convexe, c'est du lourd XD

[windows7]

J'ai pour l'instant obtenu que F et G étaient convexe, c'est du lourd XD

idem pour moi :zen:

[ffpower]

Bon, j'ai...Mais ma preuve c'est completement nimp..

[windows7]

moi j'ai sur [0,1] f est soit convexe soit concave enfait j'ai pas de resultat sur IR +

nightmare un indice ?

[ffpower]

Tu es sur que tu ne t'es pas embrouillé? f n'est effectivement défini que sur [0,1], sauf que f, c'est une variable :o)

[windows7]

je voulais parler de F

[ffpower]

ouais mais les propriétés de F dépendent essentiellement des valeurs d'arrivée de f ( et pas des valeurs de départ ), donc y'a a priori pas de raison que tu obtienne des propriétés de F juste sur [0,1]..

[windows7]

bonne remarque ! je vais re regarder tout ca, au mieu on aura la convexité ou la concavité sur IR+, c'est tjs tres peu ..

[ffpower]

Bon allez voilà ma preuve..Window7, ne regarde pas si tu veux continuer à chercher ( mais comme je l ai dit plus haut, c'est nimp vous allez voir ). Donc pour simplifier je note , . Le fait que et sont réciproques l'une de l'autre entraine que En remplaçant et par et , on a :

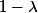
pour toute f,g continues positives, et même en fait pour toute f,g mesurable positive en utilisant de la convergence dominée. Ceci montre que la fonction vérifie une inégalité à la Jensen, et qu'elle est donc concave ( pour le vérifier, décomposer [0,1] en 2 ensembles A et B, de mesures et , puis appliquer l'inégalité pour et ).Déja à partir de là on peut récupérer la concavité de U et V. Maintenant cette fonction étant concave, sa matrice Hessienne doit être négative ( en tant que forme bilinéaire- se montre en effectuant des développements de Taylor à partir de l'inégalité de convexité ), et ceci implique que son déterminant est toujours positif ( car ses 2 valeurs propres sont négatives ), ce qui donne l'inégalité :
. Et donc maintenant c'est bidouille powaa : Par inégalité arithmético géométrique, cette derniere inégalité devient :

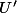
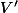
(faut faire attention au signe des différentes quantités : ,, et sont positifs, et sont négatifs )
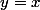
Maintenant, en dérivant 2 fois la relation , on obtient que , donc pour , l'inégalité précédente est en fait une égalité. Le cas d'égalité de l'inégalité A-M entraine ainsi :
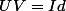
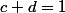
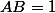
. J'en déduit que . On a donc pour une certaine constante . Je multiplie cette égalité par , et réutilise le fait que pour obtenir . Je résous cette équa diff, j'obtiens que est de la forme . Par symétrie, est aussi de la forme . L'égalité entraine que , , et la concavité ( ou la croissance, au choix ) de et entraine que A,B,c et d sont positifs. Donc au final F et G sont de la forme , , avec , , et par Holder de telles fonctions conviennent..

[Nightmare]

Hello ffpower !

c'est ce que j'ai, bien joué.

Pour la fin, je vois pas trop l'utilité d'appeler l'inégalité arithmético-géométrique :

On a effectivement U'(x)²V'(y) <= U(x)V(y)U''(x)V''(y) (1) et U''(x)V(x)+2U'(x)V'(x)+U(x)V''(x)=0 (2)

(1) avec x=y donne (U''V+UV'')²(x)=4(U'²V'²)(x) <=4(UVU''V'')(x) qui implique alors que U''V=UV''=-U'V' puis U''V+U'V'=0 et on retrouve que U'V est cste.

[windows7]

j'ai regardé vu que je pars en vacances ..
bon bah chapeau bas !

[ffpower]

Pour la fin, je vois pas trop l'utilité d'appeler l'inégalité arithmético-géométrique :

On a effectivement U'(x)²V'(y) <= U(x)V(y)U''(x)V''(y) (1) et U''(x)V(x)+2U'(x)V'(x)+U(x)V''(x)=0 (2)

(1) avec x=y donne (U''V+UV'')²(x)=4(U'²V'²)(x) <=4(UVU''V'')(x) qui implique alors que U''V=UV''=-U'V' puis U''V+U'V'=0 et on retrouve que U'V est cste.

Bah en fait c'est ce que j'avais fait au brouillon, mais je me suis dit après que je refaisais précisément la preuve de l'inégalité A-G (, donc j'ai choisi de rédiger ainsi
Mais je m'attendais pas à ce que ce soit la même preuve que toi, tellement j'ai bidouillé et avancé au hasard XD