Un petit probleme dont j'ai presque la preuve... "presque" donc pas du tout si je me veux rigoureux!
Je rappelle qu'un p-groupe G ou p est un nombre premier, est un groupe d'ordre p^m. Et c'est tout!
Soit alors un p-groupe d'ordre |G| = p^m.
Je veux alors montrer que p divise l'ordre du centre de G, |Z(G)|.
La voie relativement simple dans laquelle je me suis engagé, est de dire que d'apres Lagrange, Z(G) etant un sous groupe de G, son ordre (cad son cardinal) divise |G| et |Z(G)| s'ecrit donc p^k (0=< k =< m).
Alors si k> 0 alors p divise |Z(G)| et QED!
Mais si k=0, l'histoire reste au point mort! Je n'ai pas trouvé comment exclure le cas k=0 ou le contourner.
Merci pour toute contrib sur cette preuve ou autre preuve!
RadarX.
P-groupe
6 messages
- Page 1 sur 1
Bonjour,
On fait agir le groupe sur lui-même par conjugaison (par
sur lui-même par conjugaison (par 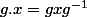 ). Notons
). Notons 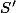 un système de représentants des classes de conjugaison, et
un système de représentants des classes de conjugaison, et 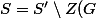) , où
, où ) est le centre de
est le centre de  . Notons enfin
. Notons enfin =\{x\in G|gx=xg\}) le centralisateur d'un élément
le centralisateur d'un élément 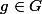 .
.
On écrit alors l'équation aux classes :
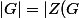|+\limits{\sum_{g\in S}[G:Z(g)]}}) .
.
Si est un
est un  -groupe,
-groupe,  divise
divise 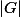 et chaque
et chaque ]) pour
pour  , il divise donc
, il divise donc |) .
.
On fait agir le groupe
On écrit alors l'équation aux classes :
Si
phenomene a écrit:Bonjour,
On fait agir le groupesur lui-même par conjugaison (par
). Notons
un système de représentants des classes de conjugaison, et
, où
est le centre de
. Notons enfin
le centralisateur d'un élément
.
On écrit alors l'équation aux classes :.
Siest un
-groupe,
divise
et chaque
pour
, il divise donc
.
Ah oui, l'equation de classes de G.... :stupid_in Parfait! Cela me va tres bien!
Merci.
RadarX.
Bonjour phenomene, ca fait plaisir de te voir sur un nouveau forum.
Après relecture de la question, je me rend compte que ma remarque est superflue, on ne demande pas que Z divise G mais que p divise Z ce qui est très légèrement différent ici, mais qui change quand même certaines choses.
Amicalement,
Quinto
Après relecture de la question, je me rend compte que ma remarque est superflue, on ne demande pas que Z divise G mais que p divise Z ce qui est très légèrement différent ici, mais qui change quand même certaines choses.
Amicalement,
Quinto
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
