Groupe cyclique

[isayama]

Bonsoir
Bon voila je trouve des difficulté pour comprendre les groupes cycliques ...y a tellement de notation que je ne me retrouve plus par exp :c est quoi la différence entre le Zn et Z/nZ ce sont tous deux des groupes cycliques

[L.A.]

Bonsoir.

A isomorphisme près, il n'y a qu'un seul groupe cyclique d'ordre n. Donc il est plus que probable que ces deux notations désignent le même groupe.

La notation la plus standard (qu'on trouve en général partout) est Z/nZ, tandis que Zn est peut être une notation spécifique de ton livre ou de ton cours. La notation Z/n existe aussi mais c'est moins répandu (et moins joli...).

[isayama]

Bonsoir.

A isomorphisme près, il n'y a qu'un seul groupe cyclique d'ordre n. Donc il est plus que probable que ces deux notations désignent le même groupe.

La notation la plus standard (qu'on trouve en général partout) est Z/nZ, tandis que Zn est peut être une notation spécifique de ton livre ou de ton cours. La notation Z/n existe aussi mais c'est moins répandu (et moins joli...).

Merci pour la réponse
Je voudrai aussi savoir la différence entre écrire le groupe cyclique avec des exponentielles
ou avec une loi de puissance

[Ben314]

Salut,
Le groupe Z/nZ, c'est le groupe quotient de (Z,+) par le sous groupe nZ. C'est donc un groupe dont la loi "naturelle" est + (en fait c'est l'addition modulo n).
Un autre modèle trés utile du groupe cyclique d'ordre n c'est de considérer les racines n-ièmes de l'unité dans le corps C des nombres complexes. C'est un groupe (cyclique d'ordre n) pour la loi x (multiplié) et il est assez souvent noté (mais d'autres notations existent). Il est (évidement) isomorphe à Z/nZ via l'application de Z/nZ dans Cn qui, à la classe de k modulo n, associe la racine n-ième .
Attention à bien comprendre que, vu que les loi sur les groupes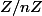 et sur sont respectivement + et x, dire que est un morphisme signifie que . De même, le neutre de 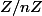est 0 alors que celui de est 1 donc on doit avoir . Enfin, le symétrique de k dans Z/nZ est -k alors que le symétrique de z dans est 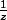donc on doit avoir