Sous-groupes de groupe cyclique

[RadarX]

Bonsoir,

Voici un resultat assez connu de la théorie des groupes:

THM: Si G est cyclique (monogene et fini) d'ordre n, alors tout ss-groupe H de G est aussi cyclique et son ordre divise n.
Inversement, pour tout diviseur d de n, G admet un [COLOR=Red]UNIQUE sous groupe (forcement cyclique) d'ordre d.[/COLOR]

Alors mon souci est au niveau de la reciproque, précisèment de l'unicité.
Voici mon debut de preuve.

Si d div n alors posons m =n/d. On montre alors facilement que est un ss-groupe (cyclique) d'ordre d; ce qui prouve l'existence!
Mais pour l'unicité d'un tel ss-groupe, je bloque un peu.

En effet j'ai supposé qu'il existe un autre ss-groupe (cyclique) d'ordre d, mais ai du mal a prouver que = ou d'aboutir à une absurdité.

Une aide ou une autre preuve m'obligerait.

Merci.

[fonfon]

Salut, je te donne quelque chose à toi de voir car j'en ai pas fait depuis quelques temps donc

Soit H un ssgroupe de G tq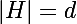
on a: d|n (je crois que c'est le th. de Lagrange)

or tu a montré que tt ssgroupe d'un groupe monogène est monogène donc on sait que H est cyclique donc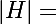 (pour un certain l)

on a (o(x)=n)

d'où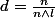 i.e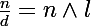

de plus (en posant

d'où

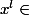d'où puis

d'où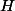

or |H|=d et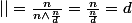

et donc devient =

A+

[yos]

Bonjour.

En effet j'ai supposé qu'il existe un autre ss-groupe (cyclique) d'ordre d, mais ai du mal a prouver que = ou d'aboutir à une absurdité.

On ne peut pas prouver que x^m=x^k car le sous-groupe n'a pas qu'un générateur en général. On doit prouver que x^k est une puissance de x^m, ça donnera l'inclusion d'un sous-groupe dans l'autre et donc l'égalité à cause des ordres égaux.

Voilà ce que je vois :
on prend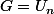 le groupe des racines n-ième de l'unité dans (tout groupe cyclique d'ordre n lui est isomorphe). Les éléments d'ordre d (où d est un diviseur fixé de n) sont racines du polynôme 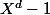, donc il y en a au plus d et les racines de ce polynôme forment évidemment un sous-groupe H de G ( 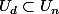). Ce sous-groupe est cyclique d'après ce que tu as déjà fait : H=.
Ainsi tout élément d'ordre d appartient à H. C'est bien ce qu'on voulait : H est l'unique sous-groupe (cyclique) d'ordre d.

Je n'ai pas lu la preuve de fonfon, mais je le ferai plus tard.

[RadarX]

La preuve de Fonfon me va bien; j'avais oublié l'hypothese "meme ordre d" qui permettait de deduire d'une inclusion , une egalité.

Je n'ai pas encore lu la preuve YOS!
Merci a vous 2.

[tize]

Je propose juste une autre démo (similaire à ce qui a déjà été ecrit) :

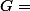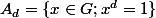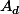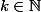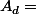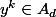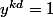Soit un groupe cyclique d'ordre et un entier divisant . il est facil de voir que est un sous groupe du groupe cyclique donc il existe tq. et puisque ,on a donc 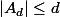et par ailleur 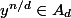est d'ordre donc 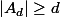et finalement 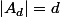et pour l'unicité il suffit de remarquer que tout sous groupe d'ordre est nécessairement inclus dans 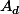(par définition de celui-ci).

[fonfon]

Tant mieux si ça a pu t'aider

A+

[RadarX]

Je propose juste une autre démo (similaire à ce qui a déjà été ecrit) :

Soit un groupe cyclique d'ordre et un entier divisant . il est facil de voir que est un sous groupe du groupe cyclique donc il existe tq. et puisque ,on a donc et par ailleur est d'ordre donc et finalement et pour l'unicité il suffit de remarquer que tout sous groupe d'ordre est nécessairement inclus dans (par définition de celui-ci).

Un peu technique celle la , mais me semble correcte. Ce seul unique sous groupe d'ordre d ne serait donc que Ad!

Big up tize.