Kazeriahm > Oui, mais l'image n'est pas le groupe des automorphismes d'un objet (ou alors je ne comprends rien)...
Nightmare > Je viens de vérifier que ce que j'ai construit est bien un isomorphisme. Ca ressemble beaucoup à la preuve du lemme de Yoneda (d'ailleurs on peut peut-être le montrer directement à partir de Yoneda, je ne sais pas...). Allons-y:
Notons
)
le morphisme défini ci-dessus, et construisons sa réciproque
 \to G)
définie comme
=\varphi(G)(1_G))
. On n'a pas besoin de vérifier que c'est un morphisme, cela proviendra du fait que c'est la réciproque de

.
Montrons que

: si
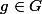
, on a
)=\Psi(\varphi_g)=\varphi_g(G)(1_G)=g \cdot 1_G=g)
: super.
Montrons que
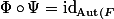})
. Là, c'est un peu plus tordu. On prend

un automorphisme de foncteur. Par définition, si

est un

-ensemble,
(E):F(E)\to F(E))
est défini par
(1_G)\cdot x)
. Par ailleurs
:F(E)\to F(E))
est définie par
(x))
. On veut donc montrer que
(1_G)\cdot x=\varphi(E)(x))
.
Pour cela, on utilise le fait que

est un morphisme de foncteurs et qu'on a à

fixé un morphisme de

-ensembles de

dans

donné par

. On lui applique le foncteur d'oubli: cela donne un diagramme commutatif que je ne peux pas dessiner ici

et qui se traduit par
(1_G)\cdot x=\varphi(E)(1_G))
, ce que l'on voulait!
Joli résultat sinon! (Et ça fait un bon exo de théorie des catégories!)
Et en plus, l'isomorphisme obtenu est fonctoriel, la classe.
