Géométrie
31 messages
- Page 1 sur 2 - 1, 2
Géométrie
Bonjour,
J'avais plusieurs questions concernant les espaces affines et la géométrie dîtes élémentaire.
J'ai trouvé dans un exercice une question : "Quelle est la nature géométrique de f" ? (Sachant que f est une application affine)
Qu'est-ce qu'on peut répondre, je n'ai aucune idée, donc savoir si c'est une symétrie ou autre, mais je les connais pas, si on pouvait me faire un petit rappel dessus, ça m'aiderait énormément.
Autres questions :
- Comment à partir d'une application f affine, on peut déterminer une similitude ?
- Comment montrer qu'une application f est une isométrie affine (directe et indirecte) ?
Puis une dernière, j'ai jamais appris ce qu'était une homothétie, j'arrive pas à comprendre ce que sait mais pire, je ne sais pas comment faire un exercice quand ça parle d'homothétie, si je pouvais avoir un rappel aussi, ça m'aiderait grandement :)
Merci à vous !
J'avais plusieurs questions concernant les espaces affines et la géométrie dîtes élémentaire.
J'ai trouvé dans un exercice une question : "Quelle est la nature géométrique de f" ? (Sachant que f est une application affine)
Qu'est-ce qu'on peut répondre, je n'ai aucune idée, donc savoir si c'est une symétrie ou autre, mais je les connais pas, si on pouvait me faire un petit rappel dessus, ça m'aiderait énormément.
Autres questions :
- Comment à partir d'une application f affine, on peut déterminer une similitude ?
- Comment montrer qu'une application f est une isométrie affine (directe et indirecte) ?
Puis une dernière, j'ai jamais appris ce qu'était une homothétie, j'arrive pas à comprendre ce que sait mais pire, je ne sais pas comment faire un exercice quand ça parle d'homothétie, si je pouvais avoir un rappel aussi, ça m'aiderait grandement :)
Merci à vous !
Salut,
Façe à une question du style "quelle est la nature de f", il y a des tonnes de truc qu'on peut regarder en fonction du contexte et du "bagage" qu'on a (i.e. de la liste de cas "connus").
1) Si tu est dans le cadre d'un espace affine Euclidien (i.e. muni d'un produit scalaire), tu peut commencer par regarder si c'est une isométrie, voire éventuellement si elle est symétrique (où plutôt si son application linéaire associée est symétrique). Si c'est une isométrie, il te faut évaluer ces propriétés (directe ? indirecte ? , si c'est une rotation son centre, ou son axe en dim. 3, son angle, etc) Si elle est symétrique, chercher les s.e.v. propres de l'application linéaire associée (en particulier celui associé à la v.p. 1 qui est lié aux éventuels point fixe de f) puis, éventuellement en déduire que c'est un objet "classique" (projection orthogonale par exemple)
2) Si tu est dans un cadre non Euclidien (i.e. pas de produit scalaire), chercher les (éventuels) points fixes et étudier l'application linéaire associée pour éventuellement tomber sur un cas "connu" (translation, symétrie, projection, homothétie, dilatation, voire plus généralement affinités) et si c'est le cas déterminer les éléments caractéristiques.
Concernant les "autres questions", déjà, ça colle pas avec le début du post, vu que pour parler d'isométrie il faut non seulement être dans le cadre d'un espace affine, mais en plus il faut qu'il soit Euclidien (i.e. que tu ait un produit scalaire) pour parler de similitude où d'isométrie.
Et concernant le "comment on fait pour..." ben la réponse est on ne peut plus con : regarde si la définition du truc est (ou pas) vérifiée :
Isométrie :,f(N))=d(M,N))
Similitude : Il existe tel que
tel que ,f(N))=k.d(M,N))
Et c'est pas con aussi, dans les exercices "pur calculatoire" de savoir repérer le truc sur la matrice A de l'application linéaire associée à f dans une base orthonormée (les preuves sont super simple et à savoir retrouver) :
Isométrie :
Similitude :
Enfin, concernant les homothéties, ça me surprend que tu ait pas déjà vu ça, au moins au collège :
Pour et
et  fixés, on appelle "homothétie de centre
fixés, on appelle "homothétie de centre  de rapport
de rapport 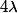 " l'application de
" l'application de 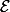 dans
dans 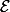 qui, à tout
qui, à tout  associe l'unique point
associe l'unique point  tel que
tel que  .
.
Façe à une question du style "quelle est la nature de f", il y a des tonnes de truc qu'on peut regarder en fonction du contexte et du "bagage" qu'on a (i.e. de la liste de cas "connus").
1) Si tu est dans le cadre d'un espace affine Euclidien (i.e. muni d'un produit scalaire), tu peut commencer par regarder si c'est une isométrie, voire éventuellement si elle est symétrique (où plutôt si son application linéaire associée est symétrique). Si c'est une isométrie, il te faut évaluer ces propriétés (directe ? indirecte ? , si c'est une rotation son centre, ou son axe en dim. 3, son angle, etc) Si elle est symétrique, chercher les s.e.v. propres de l'application linéaire associée (en particulier celui associé à la v.p. 1 qui est lié aux éventuels point fixe de f) puis, éventuellement en déduire que c'est un objet "classique" (projection orthogonale par exemple)
2) Si tu est dans un cadre non Euclidien (i.e. pas de produit scalaire), chercher les (éventuels) points fixes et étudier l'application linéaire associée pour éventuellement tomber sur un cas "connu" (translation, symétrie, projection, homothétie, dilatation, voire plus généralement affinités) et si c'est le cas déterminer les éléments caractéristiques.
Concernant les "autres questions", déjà, ça colle pas avec le début du post, vu que pour parler d'isométrie il faut non seulement être dans le cadre d'un espace affine, mais en plus il faut qu'il soit Euclidien (i.e. que tu ait un produit scalaire) pour parler de similitude où d'isométrie.
Et concernant le "comment on fait pour..." ben la réponse est on ne peut plus con : regarde si la définition du truc est (ou pas) vérifiée :
Isométrie :
Similitude : Il existe
Et c'est pas con aussi, dans les exercices "pur calculatoire" de savoir repérer le truc sur la matrice A de l'application linéaire associée à f dans une base orthonormée (les preuves sont super simple et à savoir retrouver) :
Isométrie :
Similitude :
Enfin, concernant les homothéties, ça me surprend que tu ait pas déjà vu ça, au moins au collège :
Pour
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Merci pour toutes ces précisions, j'ai un peu plus de choses qui se dessine dans mon esprit.
En fait j'ai un exercice qui est assez complet, enfin j'en ait plusieurs plus ou moins difficile mais j'essaie de faire correctement celui-là mais je bloque rapidement, j'ai des éléments de réponses, mais me manque le petit bout qui me fait avancer et conclure par la même occasion.
Soit définie par
définie par =(x+2y+2,2x-y))
1- Montrer que f est une application affine et déterminer la matrice M de sa partie linéaire l.
(J'ai pas de soucis pour cette question, j'ai trouvé la matrice d'ailleurs qui est )
)
2- Montrer que f est une similitude et préciser son rapport k. Est-elle directe ou indirecte ?
J'ai remarqué que M est de la forme avec une norme de
avec une norme de 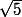
Du coup on peut "découper" cette matrice :
Le déterminant de notre nouvelle matrice que j'ai noté est de -1, donc c'est une matrice orthogonale.
est de -1, donc c'est une matrice orthogonale.
J'ai pas envie de dire de bétise, mais a première vu j'ai le rapport, une matrice orthogonale, j'ai envie de dire que cette matrice orthogonale est une isométrie, mais je sais pas pourquoi on peut le faire (si on peut le faire d'ailleurs ^^)
3) Identifier l'unique point fixe M de f.
On a un renseignement, donc on sait que 1 n'appartient pas au spectre de la matrice de la partie linéaire de f, donc après il suffit juste de résoudre=(x,y)) .
.
Donc pas de soucis.
4) Donner l'écriture en coordonnées de l'homothétie h de centre M et de rapport k. En déduire l'écriture en coordonnées de l'isométrie g telle que
En regardant ce que tu m'as dis sur les homothéties, j'ai le centre, j'ai le rapport, mais je vois pas comment se servir de ce que tu m'as dis pour répondre à la question.
Pour la deuxième partie de la question, je n'ai pas d'idée du tout.
5) Décrire géométriquement les applications g et f.
En fait j'ai un exercice qui est assez complet, enfin j'en ait plusieurs plus ou moins difficile mais j'essaie de faire correctement celui-là mais je bloque rapidement, j'ai des éléments de réponses, mais me manque le petit bout qui me fait avancer et conclure par la même occasion.
Soit
1- Montrer que f est une application affine et déterminer la matrice M de sa partie linéaire l.
(J'ai pas de soucis pour cette question, j'ai trouvé la matrice d'ailleurs qui est
2- Montrer que f est une similitude et préciser son rapport k. Est-elle directe ou indirecte ?
J'ai remarqué que M est de la forme
Du coup on peut "découper" cette matrice :
Le déterminant de notre nouvelle matrice que j'ai noté
J'ai pas envie de dire de bétise, mais a première vu j'ai le rapport, une matrice orthogonale, j'ai envie de dire que cette matrice orthogonale est une isométrie, mais je sais pas pourquoi on peut le faire (si on peut le faire d'ailleurs ^^)
3) Identifier l'unique point fixe M de f.
On a un renseignement, donc on sait que 1 n'appartient pas au spectre de la matrice de la partie linéaire de f, donc après il suffit juste de résoudre
Donc pas de soucis.
4) Donner l'écriture en coordonnées de l'homothétie h de centre M et de rapport k. En déduire l'écriture en coordonnées de l'isométrie g telle que
En regardant ce que tu m'as dis sur les homothéties, j'ai le centre, j'ai le rapport, mais je vois pas comment se servir de ce que tu m'as dis pour répondre à la question.
Pour la deuxième partie de la question, je n'ai pas d'idée du tout.
5) Décrire géométriquement les applications g et f.
Bon, au départ, c'est bon, mais ça :


Une matrice P est orthogonale ssi (équivalence) elle vérifie et ça implique (immédiatement) que det(P)=+-1 mais il est évident que le fait d'avoir un déterminant égal à +-1 est très insuffisant pour pour caractériser les matrices orthogonales :
et ça implique (immédiatement) que det(P)=+-1 mais il est évident que le fait d'avoir un déterminant égal à +-1 est très insuffisant pour pour caractériser les matrices orthogonales :
Ne jamais perdre de vu le "sens" des trucs qu'on manipule : en dim 2 par exemple si tu regarde ta matrice comme deux vecteurs colonnes (ce que tu doit presque toujours faire), le déterminant de la matrice (au signe prés), c'est l'aire du parallélogramme engendré par les deux vecteurs et dire que la matrice est orthogonale, ça veut dire que le parallélogramme en question, c'est un carré de coté 1 ce qui implique effectivement que son aire est 1, mais les parallélogrammes d'aire 1 ne sont clairement pas tous des carrés (déjà, il y a au moins les rectangles de coté a et 1/a plus... des tas d'autres !!!)
Bilan : A mon sens, ça sert pas à gras (en tout cas au départ) de diviser les coeffs de ta matrice par racine(5) mais par contre, ce que tu doit absolument faire en premier c'est de calculer : tu trouve
: tu trouve  et ça prouve que c'est une similitude de rapport
et ça prouve que c'est une similitude de rapport 
Ensuite (et seulement ensuite) tu calcule le déterminant (de P si tu a une passion pour les calculs chiants qui servent à rien, sinon... celui de M directement) tu trouve -5<0 donc c'est une similitude indirecte.
Fin de la question 2) (dans laquelle personne ne t'a parlé d'isométries ou de matrice orthogonale et où tu n'est absolument pas obligé du tout d'en parler à moins que de faire des tonnes de calculs avec du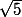 de partout ne fasse parti de tes fantasmes)
de partout ne fasse parti de tes fantasmes)
Pour le 3) : O.K. (à la limite, tu as peut-être vu ce que pouvait être une similitude indirecte dans R² ce qui te permet immédiatement de savoir à quoi t'attendre)
Pour le 4), le rapport, ben c'est évidement celui de la similitude vu que, quand tu compose des similitudes, ça multiplie leur rapport (il suffit de regarder la définition pour le voir) et qu'une isométrie, c'est une similitude de rapport 1 (même remarque) donc si f est une similitude de rapport k et que tu veut que f=goh avec g une isométrie et h une homothétie, ben faut évidement prendre h de rapport k (donc ici de rapport )
)
Et pour la deuxième partie, ben une fois que tu sait exactement qui est k, il te suffit d'écrire que
c'est LA connerie à ne pas écrire...Ncdk a écrit:Le déterminant de notre nouvelle matrice que j'ai noté... est de -1, donc c'est une matrice orthogonale.
Une matrice P est orthogonale ssi (équivalence) elle vérifie
Ne jamais perdre de vu le "sens" des trucs qu'on manipule : en dim 2 par exemple si tu regarde ta matrice comme deux vecteurs colonnes (ce que tu doit presque toujours faire), le déterminant de la matrice (au signe prés), c'est l'aire du parallélogramme engendré par les deux vecteurs et dire que la matrice est orthogonale, ça veut dire que le parallélogramme en question, c'est un carré de coté 1 ce qui implique effectivement que son aire est 1, mais les parallélogrammes d'aire 1 ne sont clairement pas tous des carrés (déjà, il y a au moins les rectangles de coté a et 1/a plus... des tas d'autres !!!)
Bilan : A mon sens, ça sert pas à gras (en tout cas au départ) de diviser les coeffs de ta matrice par racine(5) mais par contre, ce que tu doit absolument faire en premier c'est de calculer
Ensuite (et seulement ensuite) tu calcule le déterminant (de P si tu a une passion pour les calculs chiants qui servent à rien, sinon... celui de M directement) tu trouve -5<0 donc c'est une similitude indirecte.
Fin de la question 2) (dans laquelle personne ne t'a parlé d'isométries ou de matrice orthogonale et où tu n'est absolument pas obligé du tout d'en parler à moins que de faire des tonnes de calculs avec du
Pour le 3) : O.K. (à la limite, tu as peut-être vu ce que pouvait être une similitude indirecte dans R² ce qui te permet immédiatement de savoir à quoi t'attendre)
Pour le 4), le rapport, ben c'est évidement celui de la similitude vu que, quand tu compose des similitudes, ça multiplie leur rapport (il suffit de regarder la définition pour le voir) et qu'une isométrie, c'est une similitude de rapport 1 (même remarque) donc si f est une similitude de rapport k et que tu veut que f=goh avec g une isométrie et h une homothétie, ben faut évidement prendre h de rapport k (donc ici de rapport
Et pour la deuxième partie, ben une fois que tu sait exactement qui est k, il te suffit d'écrire que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
mathelot a écrit:bonsoir,
on peut classer les applications affines selon la dimension
de la variété affine constituée de leurs points fixestranslations ou glissement (??)
1 point rotations, homothétie
2 points symétrie axiale
3 points identité
sauf erreur
Fait gaffe : tout ce que tu cite là, ce sont non seulement des applications affines, mais des isométries (à part les homothéties)
Mais si tu met les homothétie dans cette "liste", il faut, à mon avis et pour des raison de cohérence donner la liste de toutes les similitudes (qui s'obtiennent par composition d'une homothétie et d'une isométrie et on peut même se débrouiller systématiquement pour que ça commute en prenant le centre de l'homothétie au "bon endroit")
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Une matrice P est orthogonale ssi (équivalence) elle vérifieet ça implique (immédiatement) que det(P)=+-1 mais il est évident que le fait d'avoir un déterminant égal à +-1 est très insuffisant pour pour caractériser les matrices orthogonales :
D'accord merci, j'ai pu voir aussi sur internet entre temps pour le produit de la transposée de la matrice avec sa matrice de base.
Ben314 a écrit:Bilan : A mon sens, ça sert pas à gras (en tout cas au départ) de diviser les coeffs de ta matrice par racine(5) mais par contre, ce que tu doit absolument faire en premier c'est de calculer: tu trouve
et ça prouve que c'est une similitude de rapport
Ensuite (et seulement ensuite) tu calcule le déterminant (de P si tu a une passion pour les calculs chiants qui servent à rien, sinon... celui de M directement) tu trouve -5<0 donc c'est une similitude indirecte.
Fin de la question 2) (dans laquelle personne ne t'a parlé d'isométries ou de matrice orthogonale et où tu n'est absolument pas obligé du tout d'en parler à moins que de faire des tonnes de calculs avec dude partout ne fasse parti de tes fantasmes)
Une question tout bête, on a trouvé que
Ensuite, c'est vrai qu'on m'a pas parlé de matrice orthogonale, mais j'avais un corrigé qui en parlé, comme ça j'ai deux manière d'y arriver sur un même exercice c'est plutôt formateur, mais j'avais fait quelques erreurs.
Ben314 a écrit:Pour le 3) : O.K. (à la limite, tu as peut-être vu ce que pouvait être une similitude indirecte dans R² ce qui te permet immédiatement de savoir à quoi t'attendre)
Je sais pas, dans mon cours ça ne traite pas ce genre de chose, je sais qu'une similitude directe conserve les angles orientés, et les similitudes indirectes c'est les autres similitudes quoi :p Mais pas de choses à ce sujet.
Ben314 a écrit:Pour le 4), le rapport, ben c'est évidement celui de la similitude vu que, quand tu compose des similitudes, ça multiplie leur rapport (il suffit de regarder la définition pour le voir) et qu'une isométrie, c'est une similitude de rapport 1 (même remarque) donc si f est une similitude de rapport k et que tu veut que f=goh avec g une isométrie et h une homothétie, ben faut évidement prendre h de rapport k (donc ici de rapport)
Et pour la deuxième partie, ben une fois que tu sait exactement qui est k, il te suffit d'écrire que
Je pense avoir compris, merci bien
Concernant le fameux  qui intervient en permanence dans tout les exercices calculatoires sur les espaces Euclidiens, y'a un truc complètement con qu'il faut avoir bien compris :
qui intervient en permanence dans tout les exercices calculatoires sur les espaces Euclidiens, y'a un truc complètement con qu'il faut avoir bien compris :
Si tu regarde M comme formée des coordonnées (en colonne) de différents vecteurs dans une quelconque base orthonormée, par exemple en dimension 3)
alors) et la règle de calcul "ligne par collone" du produit matriciel te dit que
et la règle de calcul "ligne par collone" du produit matriciel te dit que ) (en notant "." le produit scalaire)
(en notant "." le produit scalaire)
Ca ce LE TRUC A COMPRENDRE ABSOLUMENT
- D'abord parce que c'est complètement con vu qu'il suffit de savoir qu'on fait les produit "ligne par colonne" et que x1y1+x2y2+...+xnyn c'est le produit scalaire exprimé dans n'importe quelle b.o.n
- Ensuite parce que ça explique pourquoi c'est systématiquement ça qu'on calcule et ça explique aussi comment on "interprète" ce qu'on trouve.
Bon, revenons à nos moutons : ici M c'est la matrice d'une application linéaire f, donc lesvecteur qu'on "lit" dans la matrice c'est f(e1) et f(e2) (où e1,e2 c'est la base canonique et f(e1), f(e2) sont exprimés dans cette même base) donc le fait que ça signifie que f(e_1) et f(e_2) sont orthogonaux (à cause des deux 0 en dehors de la diagonale) et ça te dit aussi que ||f(e1)||²=||f(e2)||²=5 en bref, ça te dit que f(e_1),f(e_2) est une base orthogonale dont les deux vecteurs ont la même norme, à savoir racine(5).
ça signifie que f(e_1) et f(e_2) sont orthogonaux (à cause des deux 0 en dehors de la diagonale) et ça te dit aussi que ||f(e1)||²=||f(e2)||²=5 en bref, ça te dit que f(e_1),f(e_2) est une base orthogonale dont les deux vecteurs ont la même norme, à savoir racine(5).
Et ça, ça te dit que f est une similitude de rapport racine(5) (i.e. que si on composait avec une homothétie de rapport 1/racine(5) qui diviserait tout par racine(5), l'image de la base canonique serait une b.o.n. donc on aurait affaire à une isométrie)
Et si au fond, tu cherche d'où "provient", la racine carrée, ben c'est simplement du fait que dans c'est pas les norme des vecteurs u_i qu'il y a sur la diagonale, mais les carrés des normes.
c'est pas les norme des vecteurs u_i qu'il y a sur la diagonale, mais les carrés des normes.
Si tu regarde M comme formée des coordonnées (en colonne) de différents vecteurs dans une quelconque base orthonormée, par exemple en dimension 3
alors
Ca ce LE TRUC A COMPRENDRE ABSOLUMENT
- D'abord parce que c'est complètement con vu qu'il suffit de savoir qu'on fait les produit "ligne par colonne" et que x1y1+x2y2+...+xnyn c'est le produit scalaire exprimé dans n'importe quelle b.o.n
- Ensuite parce que ça explique pourquoi c'est systématiquement ça qu'on calcule et ça explique aussi comment on "interprète" ce qu'on trouve.
Bon, revenons à nos moutons : ici M c'est la matrice d'une application linéaire f, donc lesvecteur qu'on "lit" dans la matrice c'est f(e1) et f(e2) (où e1,e2 c'est la base canonique et f(e1), f(e2) sont exprimés dans cette même base) donc le fait que
Et ça, ça te dit que f est une similitude de rapport racine(5) (i.e. que si on composait avec une homothétie de rapport 1/racine(5) qui diviserait tout par racine(5), l'image de la base canonique serait une b.o.n. donc on aurait affaire à une isométrie)
Et si au fond, tu cherche d'où "provient", la racine carrée, ben c'est simplement du fait que dans
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Concernant le fameuxqui intervient en permanence dans tout les exercices calculatoires sur les espaces Euclidiens, y'a un truc complètement con qu'il faut avoir bien compris :
Si tu regarde M comme formée des coordonnées (en colonne) de différents vecteurs dans une quelconque base orthonormée, par exemple en dimension 3
alorset la règle de calcul "ligne par collone" du produit matriciel te dit que
(en notant "." le produit scalaire)
Ca ce LE TRUC A COMPRENDRE ABSOLUMENT
- D'abord parce que c'est complètement con vu qu'il suffit de savoir qu'on fait les produit "ligne par colonne" et que x1y1+x2y2+...+xnyn c'est le produit scalaire exprimé dans n'importe quelle b.o.n
- Ensuite parce que ça explique pourquoi c'est systématiquement ça qu'on calcule et ça explique aussi comment on "interprète" ce qu'on trouve.
Bon, revenons à nos moutons : ici M c'est la matrice d'une application linéaire f, donc lesvecteur qu'on "lit" dans la matrice c'est f(e1) et f(e2) (où e1,e2 c'est la base canonique et f(e1), f(e2) sont exprimés dans cette même base) donc le fait queça signifie que f(e_1) et f(e_2) sont orthogonaux (à cause des deux 0 en dehors de la diagonale) et ça te dit aussi que ||f(e1)||²=||f(e2)||²=5 en bref, ça te dit que f(e_1),f(e_2) est une base orthogonale dont les deux vecteurs ont la même norme, à savoir racine(5).
Et ça, ça te dit que f est une similitude de rapport racine(5) (i.e. que si on composait avec une homothétie de rapport 1/racine(5) qui diviserait tout par racine(5), l'image de la base canonique serait une b.o.n. donc on aurait affaire à une isométrie)
Et si au fond, tu cherche d'où "provient", la racine carrée, ben c'est simplement du fait que dansc'est pas les norme des vecteurs u_i qu'il y a sur la diagonale, mais les carrés des normes.
Excellent merci pour tes explications clair, et merci à mathelot pour la classification des isométries, j'en ait profité pour le marquer sur une fiche
Je reviens sur l'exercice que j'ai posé plus haut juste pour savoir quelque chose, j'ai trouvé donc mon application g, quand je fais sa partie linéaire j'obtiens exactement la matrice que j'avais noté P plus haut ? Est-ce une coïncidence ?
Je pense pas personnellement mais je n'arrive pas à trouver le lien entre ce que j'ai fait avant, et ce résultat obtenu à la fin...
Je pense pas personnellement mais je n'arrive pas à trouver le lien entre ce que j'ai fait avant, et ce résultat obtenu à la fin...
C'est tout à fait normal.
Le fait que les applications affines f,g,h vérifient implique (mais ce n'est pas équivalent) que les applications linéaires associées
implique (mais ce n'est pas équivalent) que les applications linéaires associées  vérifient
vérifient  c'est à dire,
c'est à dire, ) si M,N,H sont les matrices respectives des applications linéaires
si M,N,H sont les matrices respectives des applications linéaires  .
.
Sauf que, si h est une homothétie de centre quelconque et de rapport k alors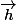 c'est l'application linéaire x->k.x (et on perd l'info. concernant le centre). Si ce n'est pas évident pour toi, démontre le en utilisant la définition "d'application linéaire associé".
c'est l'application linéaire x->k.x (et on perd l'info. concernant le centre). Si ce n'est pas évident pour toi, démontre le en utilisant la définition "d'application linéaire associé".
Et tu en profite pour montrer que, réciproquement, si h est une application affine telle que, pour tout vecteur x on ait=k.x) avec k différent de 1, alors h est forcément une homothétie de rapport k et (de centre on sait pas trop quoi). Qu'en est-il dans la cas où k=1 ?
avec k différent de 1, alors h est forcément une homothétie de rapport k et (de centre on sait pas trop quoi). Qu'en est-il dans la cas où k=1 ?
C'est à mon avis un truc indispensable "à savoir" vu que c'est la base de tout concernant les similitudes (vu que les similitudes sont les composées d'isométries et d'homothéties)
Bilan : la matrice H de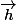 , c'est
, c'est  avec
avec  et l'égalité
et l'égalité ) dit en fait que
dit en fait que  c'est à dire que
c'est à dire que  ce qui fait... qu'on retourne à la case départ, c'est à dire au 2) où on avait vu que
ce qui fait... qu'on retourne à la case départ, c'est à dire au 2) où on avait vu que  et donc que, si on pose
et donc que, si on pose  on a
on a  ce qui signifiait dés le départ que N est la matrice de l'application linéaire associée à une isométrie.
ce qui signifiait dés le départ que N est la matrice de l'application linéaire associée à une isométrie.
Le fait que les applications affines f,g,h vérifient
Sauf que, si h est une homothétie de centre quelconque et de rapport k alors
Et tu en profite pour montrer que, réciproquement, si h est une application affine telle que, pour tout vecteur x on ait
C'est à mon avis un truc indispensable "à savoir" vu que c'est la base de tout concernant les similitudes (vu que les similitudes sont les composées d'isométries et d'homothéties)
Bilan : la matrice H de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:C'est tout à fait normal.
Le fait que les applications affines f,g,h vérifientimplique (mais ce n'est pas équivalent) que les applications linéaires associées
vérifient
c'est à dire,
si M,N,H sont les matrices respectives des applications linéaires
.
Sauf que, si h est une homothétie de centre quelconque et de rapport k alorsc'est l'application linéaire x->k.x (et on perd l'info. concernant le centre). Si ce n'est pas évident pour toi, démontre le en utilisant la définition "d'application linéaire associé".
Et tu en profite pour montrer que, réciproquement, si h est une application affine telle que, pour tout vecteur x on aitavec k différent de 1, alors h est forcément une homothétie de rapport k et (de centre on sait pas trop quoi). Qu'en est-il dans la cas où k=1 ?
C'est à mon avis un truc indispensable "à savoir" vu que c'est la base de tout concernant les similitudes (vu que les similitudes sont les composées d'isométries et d'homothéties)
Bilan : la matrice H de, c'est
avec
et l'égalité
dit en fait que
c'est à dire que
ce qui fait... qu'on retourne à la case départ, c'est à dire au 2) où on avait vu que
et donc que, si on pose
on a
ce qui signifiait dés le départ que N est la matrice de l'application linéaire associée à une isométrie.
Ah oui je vois, d'accord, dire que j'avais trouvé la fin de l'exercice sans le savoir :marteau:
C'est peut-être d'ailleurs la raison pourquoi mon prof a fait cette méthode, pour trouver P et qu'au final à la fin on puisse s'en servir.
Une dernière chose, j'avais un autre exercice mais c'est plus une question en particulier qui me pose problème et même les symétries en général, je vois ce que c'est sur un dessin, mais faire le lien avec des expressions littérales, ça me bloque complet :hein:
Soit
1) Montrer que f est une isométrie affine indirecte et expliciter sa partie linéaire l (Fait sans soucis)
2) Montrer que l est une symétrie orthogonale et expliciter ses éléments caractéristiques
C'est cette question qui m'embête, j'ai la matrice associée a la partie linéaire de f.
Je sais pas tellement quoi faire avec, j'avais une idée, celle de voir si déjà si c'est une matrice orthogonale, vu que ça parle d'orthogonalité, mais pour prouver que c'est une symétrie orthogonale je vois pas, mais surtout je vois sur quoi aboutir. Concrétement, je sais pas à quoi je dois arriver pour dire "Ce résultat implique ou est équivalent à dire que la partie linéaire est une symétrie orthogonale".
Ce genre de question, y'a des tonnes de façon de le traiter en fonction du "bagage" qu'on a.
Bon, déjà, une "symétrie vectorielle" (cas non Euclidien), faudrait savoir ce que c'est :
I) Lorsque tu as un espace vectoriel quelconque E qui est somme directe de deux s.e.v. F et G,
1) L'application (
( évidement) est appelée "projection sur F parallèlement à G".
évidement) est appelée "projection sur F parallèlement à G".
Sa matrice dans une base adaptée (formée de la réunion d'une base de F et d'une base de G) est clairement une matrice diagonale avec des 1 sur la diagonale (pour les vecteurs de la base de F) puis des 0 (pour ceux de la base de G).
Un exercce plus que classique d'algèbre linéaire consiste à montrer qu'un endomorphisme p est une projection ssi pop=p (c'est alors la projection sur Im(p)=Ker(Id-p) parallèlement à Ker(p)=Im(Id-p) qui sont obligatoirement supplémentaires). Ca veut dire que, si tu as la matrice P de p dans une base pas forcément adaptée, pour voir si c'est une projection, il faut regarder si P²=P (ou pas) puis, si c'est le cas, pour avoir les "éléments caractéristiques", c'est à dire F et G, ben il faut calculer Im(p) et Ker(p).
2) L'application (
( évidement) est appelée "symétrie par rapport à F parallèlement à G".
évidement) est appelée "symétrie par rapport à F parallèlement à G".
Sa matrice dans une base adaptée (formée de la réunion d'une base de F et d'une base de G) est clairement une matrice diagonale avec des 1 sur la diagonale (pour les vecteurs de la base de F) puis des -1 (pour ceux de la base de G).
Un exercice plus que classique d'algèbre linéaire consiste à montrer qu'un endomorphisme s est une symétrie ssi sos=Id (c'est alors la symétrie par rapport à Ker(s-Id)=Im(s+Id) parallèlement à Ker(s+Id)=Im(s-Id) qui sont obligatoirement supplémentaires). Ca veut dire que, si tu as la matrice M de s dans une base pas forcément adaptée, pour voir si c'est une symétrie, il faut regarder si S²=S (ou pas) puis, si c'est le cas, pour avoir les "éléments caractéristiques", c'est à dire F et G, ben il faut calculer Ker(s-Id)=Im(s+Id) ainsi que Ker(s+Id)=Im(s-Id)
Rien qu'avec ça, tu peut parfaitement faire l'exo mais... c'est super long et trés con vu que tu utilise pas du tout le coté "orthogonal" du bidule (i.e. le caractère Euclidien de ton espace)
Comme c'est long je te fait un deuxième post...
Bon, déjà, une "symétrie vectorielle" (cas non Euclidien), faudrait savoir ce que c'est :
I) Lorsque tu as un espace vectoriel quelconque E qui est somme directe de deux s.e.v. F et G,
1) L'application
Sa matrice dans une base adaptée (formée de la réunion d'une base de F et d'une base de G) est clairement une matrice diagonale avec des 1 sur la diagonale (pour les vecteurs de la base de F) puis des 0 (pour ceux de la base de G).
Un exercce plus que classique d'algèbre linéaire consiste à montrer qu'un endomorphisme p est une projection ssi pop=p (c'est alors la projection sur Im(p)=Ker(Id-p) parallèlement à Ker(p)=Im(Id-p) qui sont obligatoirement supplémentaires). Ca veut dire que, si tu as la matrice P de p dans une base pas forcément adaptée, pour voir si c'est une projection, il faut regarder si P²=P (ou pas) puis, si c'est le cas, pour avoir les "éléments caractéristiques", c'est à dire F et G, ben il faut calculer Im(p) et Ker(p).
2) L'application
Sa matrice dans une base adaptée (formée de la réunion d'une base de F et d'une base de G) est clairement une matrice diagonale avec des 1 sur la diagonale (pour les vecteurs de la base de F) puis des -1 (pour ceux de la base de G).
Un exercice plus que classique d'algèbre linéaire consiste à montrer qu'un endomorphisme s est une symétrie ssi sos=Id (c'est alors la symétrie par rapport à Ker(s-Id)=Im(s+Id) parallèlement à Ker(s+Id)=Im(s-Id) qui sont obligatoirement supplémentaires). Ca veut dire que, si tu as la matrice M de s dans une base pas forcément adaptée, pour voir si c'est une symétrie, il faut regarder si S²=S (ou pas) puis, si c'est le cas, pour avoir les "éléments caractéristiques", c'est à dire F et G, ben il faut calculer Ker(s-Id)=Im(s+Id) ainsi que Ker(s+Id)=Im(s-Id)
Rien qu'avec ça, tu peut parfaitement faire l'exo mais... c'est super long et trés con vu que tu utilise pas du tout le coté "orthogonal" du bidule (i.e. le caractère Euclidien de ton espace)
Comme c'est long je te fait un deuxième post...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
II) Dans le cas d'un espace vectoriel Euclidien et de projection/symétries orthogonale, c'est exactement les mêmes définitions, sauf qu'on prend forcément  donc c'est plus la peine d'écrire "parallèlement à G" vu que c'est forcément "parallèlement à
donc c'est plus la peine d'écrire "parallèlement à G" vu que c'est forcément "parallèlement à  ".
".
Pour les matrices dans des "bases adaptées", c'est pareil sauf que les "bases adaptées" sont orthonormées (réunion de b.o.n de F et de G).
Concernant la caractérisation pop=p et fof=Id, c'est évidement la même chose avec une propriété supplémentaire (pour traduire le fait que ), à savoir que p doit être un endomorphisme symétrique (i.e. p(x).y=x.p(y) pour tout vecteurs x et y de E : tu prouve en une demi ligne que ça équivaut à " Ker(p) orthogonal à Im(p)") et que s est un endomorphisme symétrique (même remarque avec cette fois Ker(s-Id) et Im(s-id)) ET/OU que s est une isométrie (même remarque) let ET/OU provien du fait qu'il suffit de montrer un des deux pour avoir les deux.
), à savoir que p doit être un endomorphisme symétrique (i.e. p(x).y=x.p(y) pour tout vecteurs x et y de E : tu prouve en une demi ligne que ça équivaut à " Ker(p) orthogonal à Im(p)") et que s est un endomorphisme symétrique (même remarque avec cette fois Ker(s-Id) et Im(s-id)) ET/OU que s est une isométrie (même remarque) let ET/OU provien du fait qu'il suffit de montrer un des deux pour avoir les deux.
En terme de matrice dans un base orthonormée (pas forcément adaptée), pour les projection, on doit donc avoir P²=P et P symétrique et, pour les symétries, S²=S et S symétrique (cette deuxième condition pouvant être remplacée par ).
).
Concernant les "élément caractéristiques", même chose que dans le cas "non euclidien" sauf que, dés qu'on a calculé un des deux s.e.v. F ou G, on a directement l'autre vu que c'est l'orthogonal.
Pour les matrices dans des "bases adaptées", c'est pareil sauf que les "bases adaptées" sont orthonormées (réunion de b.o.n de F et de G).
Concernant la caractérisation pop=p et fof=Id, c'est évidement la même chose avec une propriété supplémentaire (pour traduire le fait que
En terme de matrice dans un base orthonormée (pas forcément adaptée), pour les projection, on doit donc avoir P²=P et P symétrique et, pour les symétries, S²=S et S symétrique (cette deuxième condition pouvant être remplacée par
Concernant les "élément caractéristiques", même chose que dans le cas "non euclidien" sauf que, dés qu'on a calculé un des deux s.e.v. F ou G, on a directement l'autre vu que c'est l'orthogonal.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
III) Dans le cas d'un espace affine Euclidien, là, il faut évidement changer les définitions vu que "sous espaces affines supplémentaires" ça veut rien dire et qu'on peut pas ajouter des points.
Donc on suppose qu'on a un sous espace affine G de l'espace affine Euclidien E et que G est dirigé par le s.e.v.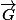 .
.
On montre facilement qu'étant donné un point M quelconque de E, le sous espace affine passant par M et dirigé par coupe le sous espace affine G en un unique point N appelé "projeté orthogonal de M sur G".
coupe le sous espace affine G en un unique point N appelé "projeté orthogonal de M sur G".
L'unique point N' tel que N soit le milieu de [MN'] est appelé "symétrique (orthogonal) de M par rapport à G".
On vérifie ensuite que ce sont bien des applications affines et que les applications linéaires associés sont bien des projection orthogonales et des symétries orthogonales (vectorielles).
Une caractérisation des projection est pop=p (attention, si l'application linéaire associée vérifie , ce n'est pas suffisant) ET l'application linéaire associée est symétrique.
, ce n'est pas suffisant) ET l'application linéaire associée est symétrique.
Une caractérisation des symétries est sos=s (même remarque) ET l'application linéaire associée est symétrique (ET/OU c'est une isométrie).
Donc on suppose qu'on a un sous espace affine G de l'espace affine Euclidien E et que G est dirigé par le s.e.v.
On montre facilement qu'étant donné un point M quelconque de E, le sous espace affine passant par M et dirigé par
L'unique point N' tel que N soit le milieu de [MN'] est appelé "symétrique (orthogonal) de M par rapport à G".
On vérifie ensuite que ce sont bien des applications affines et que les applications linéaires associés sont bien des projection orthogonales et des symétries orthogonales (vectorielles).
Une caractérisation des projection est pop=p (attention, si l'application linéaire associée vérifie
Une caractérisation des symétries est sos=s (même remarque) ET l'application linéaire associée est symétrique (ET/OU c'est une isométrie).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Revenons (enfin) à l'exo.
Vu qu'au 1) tu as montré déjà montré que f était une isométrie, pour montrer que c'est une symétrie orthogonale, il y a plein de choses qu'on peut faire :
1) Montrer que fof=Id avec deux méthodes :
1.1) Calculer "pour de vrai" fof.
1.2) Calculer le carré de la matrice de l'application linéaire associé à f : c'est bien plus rapide MAIS ça ne montre pas exactement ce qu'il faut. En fait, ca montre que l'application linéaire associée à fof est Id, c'est à dire que fof est une translation et il reste à montrer que c'est en fait une translation de vecteur nul. Pour ce faire, il suffit de calculer fof de un seul point (par exemple (0,0)) et de vérifier qu'on retombe sur le point de départ.
2) Regarder dans le blanc des yeux la matrice S de l'application linéaire associée à f et constater qu'elle est symétrique (ça c'est cool : ça va vite...). Comme tu as montré au 1) que le fait qu'en plus
le fait qu'en plus  montre que
montre que  donc l'application linéaire associée à f est une symétrie. Mais attention (bis et répétita), ça ne prouve pas que f est une symétrie . De nouveau, tout ce qu'on sait, c'est que l'application linéaire associée à fof est Id donc que fof est une translation. Pour montrer que c'est effectivement Id il suffit de calculer fof de un point (par exemple (0,0)
donc l'application linéaire associée à f est une symétrie. Mais attention (bis et répétita), ça ne prouve pas que f est une symétrie . De nouveau, tout ce qu'on sait, c'est que l'application linéaire associée à fof est Id donc que fof est une translation. Pour montrer que c'est effectivement Id il suffit de calculer fof de un point (par exemple (0,0)
Reste à déterminer les "éléments caractéristiques" ce qui, ici se résume à chercher le sous espace affine G par rapport auquel on a fait la symétrie.
La façon la plus simple (dans les cas calculatoires) de le trouver c'est évidement de dire que c'est l'ensemble des points invariants par f, c'est à dire de résoudre f(M)=M.
A la limite, avant de se lancer dans les calculs, on peut souvent facilement avoir la dimension de G dans ce type d'exo : on sait que, dans une b.o.n. "adaptée", la matrice de l'application linéaire associée à f est diagonale avec des 1 et des -1 sur la diagonale (avec dim(G)=nombre de 1).
- Ca peut pas être 3 "1" sinon l'application linéaire associés serait Id, donc f serait une translation et on aurait repéré ça du premier coup d'oeil vu que f aurait été de la forme (x,y,z)->(x+Cst,y+Cst,z+Cst)
- Ca peut pas être 3 "-1" (i.e. G de dim 0, c'est à dire G={Mo} : symétrie "centrale") vu que ça se repèrerais aussi du 1et coup d'oeil : f serait de la forme (x,y,z)->(-x+Cst,-y+Cst,-z+Cst)
- Il y a donc un ou deux "1" (symétrie par rapport à une droite ou par rapport à un plan) sauf que, au 1) tu as montré que c'était une isométrie indirecte donc de déterminant -1 dans n'importe quelle base ce qui signifie qu'il y a 2 "1" sur la diagonale (et un seul -1) => G est un plan affine.
Vu qu'au 1) tu as montré déjà montré que f était une isométrie, pour montrer que c'est une symétrie orthogonale, il y a plein de choses qu'on peut faire :
1) Montrer que fof=Id avec deux méthodes :
1.1) Calculer "pour de vrai" fof.
1.2) Calculer le carré de la matrice de l'application linéaire associé à f : c'est bien plus rapide MAIS ça ne montre pas exactement ce qu'il faut. En fait, ca montre que l'application linéaire associée à fof est Id, c'est à dire que fof est une translation et il reste à montrer que c'est en fait une translation de vecteur nul. Pour ce faire, il suffit de calculer fof de un seul point (par exemple (0,0)) et de vérifier qu'on retombe sur le point de départ.
2) Regarder dans le blanc des yeux la matrice S de l'application linéaire associée à f et constater qu'elle est symétrique (ça c'est cool : ça va vite...). Comme tu as montré au 1) que
Reste à déterminer les "éléments caractéristiques" ce qui, ici se résume à chercher le sous espace affine G par rapport auquel on a fait la symétrie.
La façon la plus simple (dans les cas calculatoires) de le trouver c'est évidement de dire que c'est l'ensemble des points invariants par f, c'est à dire de résoudre f(M)=M.
A la limite, avant de se lancer dans les calculs, on peut souvent facilement avoir la dimension de G dans ce type d'exo : on sait que, dans une b.o.n. "adaptée", la matrice de l'application linéaire associée à f est diagonale avec des 1 et des -1 sur la diagonale (avec dim(G)=nombre de 1).
- Ca peut pas être 3 "1" sinon l'application linéaire associés serait Id, donc f serait une translation et on aurait repéré ça du premier coup d'oeil vu que f aurait été de la forme (x,y,z)->(x+Cst,y+Cst,z+Cst)
- Ca peut pas être 3 "-1" (i.e. G de dim 0, c'est à dire G={Mo} : symétrie "centrale") vu que ça se repèrerais aussi du 1et coup d'oeil : f serait de la forme (x,y,z)->(-x+Cst,-y+Cst,-z+Cst)
- Il y a donc un ou deux "1" (symétrie par rapport à une droite ou par rapport à un plan) sauf que, au 1) tu as montré que c'était une isométrie indirecte donc de déterminant -1 dans n'importe quelle base ce qui signifie qu'il y a 2 "1" sur la diagonale (et un seul -1) => G est un plan affine.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Merci pour toutes les explications, ça m'a pas mal rappelé les exercices fait en algébre linéaire sur les projecteurs, on avait fait ça avec nos acquis sur les espaces vectoriels, mais c'est vrai qu'on nous avait pas expliqué le point de vue géométrique qui se caché derrière, peut-être qu'on avait pas assez de bagage encore pour le comprendre.
Pour revenir à l'exercice :
En fait, avec les matrices ce qu'on montre c'est juste que l'application linéaire de f est une symétrie, mais au final ce qu'il faut faire c'est de quand même calculer fof, puis de trouver sa partie linéaire, de bien voir que c'est Id et pour finir, on calcule f(f(0,0,0)) mais il faut que l'on retombe sur Id non ?
Du coup pour trouver les éléments caractéristiques, ça revient à trouver les points fixes, du coup est-ce que chercher les sous-espaces propres, on devrait en avoir 3 car tu m'as parlé de matrice diagonale, même que la matrice de la partie linéaire de f est diagonale, donc du coup si au final on obtient 3 vecteurs, qui forment une base et que ces vecteurs sont deux à deux orthogonaux, qu'est-ce que ça prouverait, qu'on a une base orthogonale et que nos sous espace propres sont orthogonaux ?
Pour revenir à l'exercice :
Ben314 a écrit:2) Regarder dans le blanc des yeux la matrice S de l'application linéaire associée à f et constater qu'elle est symétrique (ça c'est cool : ça va vite...). Comme tu as montré au 1) quele fait qu'en plus
montre que
donc l'application linéaire associée à f est une symétrie. Mais attention (bis et répétita), ça ne prouve pas que f est une symétrie . De nouveau, tout ce qu'on sait, c'est que l'application linéaire associée à fof est Id donc que fof est une translation. Pour montrer que c'est effectivement Id il suffit de calculer fof de un point (par exemple (0,0)
En fait, avec les matrices ce qu'on montre c'est juste que l'application linéaire de f est une symétrie, mais au final ce qu'il faut faire c'est de quand même calculer fof, puis de trouver sa partie linéaire, de bien voir que c'est Id et pour finir, on calcule f(f(0,0,0)) mais il faut que l'on retombe sur Id non ?
Du coup pour trouver les éléments caractéristiques, ça revient à trouver les points fixes, du coup est-ce que chercher les sous-espaces propres, on devrait en avoir 3 car tu m'as parlé de matrice diagonale, même que la matrice de la partie linéaire de f est diagonale, donc du coup si au final on obtient 3 vecteurs, qui forment une base et que ces vecteurs sont deux à deux orthogonaux, qu'est-ce que ça prouverait, qu'on a une base orthogonale et que nos sous espace propres sont orthogonaux ?
Concernant le fait que f est une symétrie, je t'ai tout écrit au dessus : si tu montre que l'application linéaire associée est une symétrie (soit en calculant le carré de la matrice, soit plus simplement en vérifiant qu'elle est symétrique), il te reste uniquement à vérifier que (par exemple) fof(0,0,0)=(0,0,0) pour conclure vu qu'une translation admettant un point fixe, c'est clairement l'identité.
Concernant la recherche de G, je vois pas trop l'intérêt de chercher les sous espaces propres :
1) Tu sait d'avance (et avec quasi aucun calculs(*)) ce que tu va trouver, à savoir deux valeurs propres 1 et -1 avec des s.e.propres associées qui sont orthogonaux.
2) Cherche les deux sous espaces propres (associés à 1 et -1) est un peu con vu que tu sait qu'ils sont orthogonaux donc la connaissance d'un des deux est bien suffisante (sans parler qu'il y en a forcément un des 2 qui est de dim 2 et il va falloir t'emmerder à en choisir une base)
3) Une fois que tu aura fait ça, tu n'aura même pas fini, vu que tu ne connaitra que le s.e.v. directeur du s.e.affine G par rapport à qui on a fait une symétrie et il te faudra en plus trouver un point de G, et la façon simple de le trouver sera de trouver une solution de l'équation f(M)=M.
Bilan : tu ne coupera pas à résoudre (au moins un minimum) l'équation f(M)=M donc, tant qu'à faire, tu la résoud entièrement, et... tu ne fait rien d'autre vu que c'est fini : tu as les équations de G sous les yeux.
A la rigueur, là que tu as le temps, tu peut faire tout les calculs (polynôme caractéristique et tout le bastringue) pour vérifier que tout est bien conforme à ce que la théorie dit. Mais un jour d'exam. si tu fait ça, ça te prend 10 fois le temps normal nécessaire à la résolution de l'exercice...
(*) En fait, connaissant la matrice d'une symétrie vectorielle, le lus rapide pour déterminer la dimension du s.e.v. par rapport à qui on a fait une symétrie, c'est plutôt d'utiliser la trace que le déterminant. Comme elle est invariante pas rchangement de base, c'est la même que dans la "base adaptée" où la matrice est diagonale avec des 1 et de -1 sur la diagonale. Par exemple ta matrice a une trace=1 donc =1+1+(-1) [pas d'autre possibilité avec 3 "1" ou "-1"] donc dim(G)=2.
Concernant la recherche de G, je vois pas trop l'intérêt de chercher les sous espaces propres :
1) Tu sait d'avance (et avec quasi aucun calculs(*)) ce que tu va trouver, à savoir deux valeurs propres 1 et -1 avec des s.e.propres associées qui sont orthogonaux.
2) Cherche les deux sous espaces propres (associés à 1 et -1) est un peu con vu que tu sait qu'ils sont orthogonaux donc la connaissance d'un des deux est bien suffisante (sans parler qu'il y en a forcément un des 2 qui est de dim 2 et il va falloir t'emmerder à en choisir une base)
3) Une fois que tu aura fait ça, tu n'aura même pas fini, vu que tu ne connaitra que le s.e.v. directeur du s.e.affine G par rapport à qui on a fait une symétrie et il te faudra en plus trouver un point de G, et la façon simple de le trouver sera de trouver une solution de l'équation f(M)=M.
Bilan : tu ne coupera pas à résoudre (au moins un minimum) l'équation f(M)=M donc, tant qu'à faire, tu la résoud entièrement, et... tu ne fait rien d'autre vu que c'est fini : tu as les équations de G sous les yeux.
A la rigueur, là que tu as le temps, tu peut faire tout les calculs (polynôme caractéristique et tout le bastringue) pour vérifier que tout est bien conforme à ce que la théorie dit. Mais un jour d'exam. si tu fait ça, ça te prend 10 fois le temps normal nécessaire à la résolution de l'exercice...
(*) En fait, connaissant la matrice d'une symétrie vectorielle, le lus rapide pour déterminer la dimension du s.e.v. par rapport à qui on a fait une symétrie, c'est plutôt d'utiliser la trace que le déterminant. Comme elle est invariante pas rchangement de base, c'est la même que dans la "base adaptée" où la matrice est diagonale avec des 1 et de -1 sur la diagonale. Par exemple ta matrice a une trace=1 donc =1+1+(-1) [pas d'autre possibilité avec 3 "1" ou "-1"] donc dim(G)=2.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Concernant le fait que f est une symétrie, je t'ai tout écrit au dessus : si tu montre que l'application linéaire associée est une symétrie (soit en calculant le carré de la matrice, soit plus simplement en vérifiant qu'elle est symétrique), il te reste uniquement à vérifier que (par exemple) fof(0,0,0)=(0,0,0) pour conclure vu qu'une translation admettant un point fixe, c'est clairement l'identité.
Concernant la recherche de G, je vois pas trop l'intérêt de chercher les sous espaces propres :
1) Tu sait d'avance (et avec quasi aucun calculs(*)) ce que tu va trouver, à savoir deux valeurs propres 1 et -1 avec des s.e.propres associées qui sont orthogonaux.
2) Cherche les deux sous espaces propres (associés à 1 et -1) est un peu con vu que tu sait qu'ils sont orthogonaux donc la connaissance d'un des deux est bien suffisante (sans parler qu'il y en a forcément un des 2 qui est de dim 2 et il va falloir t'emmerder à en choisir une base)
3) Une fois que tu aura fait ça, tu n'aura même pas fini, vu que tu ne connaitra que le s.e.v. directeur du s.e.affine G par rapport à qui on a fait une symétrie et il te faudra en plus trouver un point de G, et la façon simple de le trouver sera de trouver une solution de l'équation f(M)=M.
Bilan : tu ne coupera pas à résoudre (au moins un minimum) l'équation f(M)=M donc, tant qu'à faire, tu la résoud entièrement, et... tu ne fait rien d'autre vu que c'est fini : tu as les équations de G sous les yeux.
A la rigueur, là que tu as le temps, tu peut faire tout les calculs (polynôme caractéristique et tout le bastringue) pour vérifier que tout est bien conforme à ce que la théorie dit. Mais un jour d'exam. si tu fait ça, ça te prend 10 fois le temps normal nécessaire à la résolution de l'exercice...
(*) En fait, connaissant la matrice d'une symétrie vectorielle, le lus rapide pour déterminer la dimension du s.e.v. par rapport à qui on a fait une symétrie, c'est plutôt d'utiliser la trace que le déterminant. Comme elle est invariante pas rchangement de base, c'est la même que dans la "base adaptée" où la matrice est diagonale avec des 1 et de -1 sur la diagonale. Par exemple ta matrice a une trace=1 donc =1+1+(-1) [pas d'autre possibilité avec 3 "1" ou "-1"] donc dim(G)=2.
Super merci pour ton aide plus que complète
31 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
