Bonjour, j'ai un exercice de géométrie mais je n'arrive pas à le résoudre :
Dans le plan affine on se donne six points distincts deux à deux et on suppose : (AC') // (BA') // (CB') et (A'C) // (B'A) // (C'B)
Il faut montrer que (AA'), (BB') et (CC') sont soit coucourantes soit parallèles.
Je voulais partir du fait que deux droites sont parallèles, leurs vecteurs directeurs sont égaux mais je n'arrive pas à continuer.
Merci
Géométrie
11 messages
- Page 1 sur 1
marion79 a écrit:Bonjour, j'ai un exercice de géométrie mais je n'arrive pas à le résoudre :
Dans le plan affine on se donne six points distincts deux à deux et on suppose : (AC') // (BA') // (CB') et (A'C) // (B'A) // (C'B)
Il faut montrer que (AA'), (BB') et (CC') sont soit coucourantes soit parallèles.
Je voulais partir du fait que deux droites sont parallèles, leurs vecteurs directeurs sont égaux mais je n'arrive pas à continuer.
Merci
Bj
pour faire une figure, trace 3 droites parallèles puis 3 autres droites parallèles d'une autre direction.
tu obtiens 9 points d'intersection. Place tes 6 points parmi les 9 de sorte que les hypothèses soient vérifiées. Ce sera plus clair.
Maxmau a écrit:Bj
pour faire une figure, trace 3 droites parallèles puis 3 autres droites parallèles d'une autre direction.
tu obtiens 9 points d'intersection. Place tes 6 points parmi les 9 de sorte que les hypothèses soient vérifiées. Ce sera plus clair.
En fixant un repère comme (A, AB', AC') et en posant A'(m,p) on arrive assez facilement à trouver les équations des droites (en fonction de m et p) et à montrer qu'elles sont concourantes ou parallèles mais il doit y avoir quelque chose de mieux :hum:
vois du côté de Desargues, peut-être
chan79 a écrit:En fixant un repère comme (A, AB', AC') et en posant A'(m,p) on arrive assez facilement à trouver les équations des droites (en fonction de m et p) et à montrer qu'elles sont concourantes ou parallèles mais il doit y avoir quelque chose de mieux :hum:
vois du côté de Desargues, peut-être
La solution analytique n'est pas bien difficile
on peut aussi envisager une solution plus "géométrie pure" utilisant les propriétés de la projection centrale d'une droite sur une droite
Sans doute y-a-t'il encore d'autres points de vue
chan79 a écrit:En fixant un repère comme (A, AB', AC') et en posant A'(m,p) on arrive assez facilement à trouver les équations des droites (en fonction de m et p) et à montrer qu'elles sont concourantes ou parallèles mais il doit y avoir quelque chose de mieux :hum:
vois du côté de Desargues, peut-être
Bj
C'est à vérifier mais je crois que c'est un cas particulier du dual du théorème de Pappus
marion79 a écrit:je ne vois pas du tout comment faire :/
PAPPUS dual
Le plan usuel est complété par ses points à linfini
(CA) , (AB) , (BC) concourantes en J (éventuellement à linfini)
(AC) , (BA) , (CB) concourantes en I ( éventuellement à linfini)
Montrer que (AA) , (BB) , (CC) concourantes ou parallèles
Solution:
O : point dintersection des droites (CB) et (CB)
Soit p la projection de centre C de (CB) sur ( BB) ,
q la projection de centre A de (BB) sur (BA)
r la projection de (CB) sur (BA) de centre I
Les transformations qop et r conservent le birapport et coincident en 3 points ( O , B , J) , elles sont donc égales.
En particulier: [qop] ( C ) = r( C ) qui donne le résultat souhaité
Rem: Dans le cas I et J à linfini on retrouve lexo
maintenant pour ton exo tu as la solution analytique
marion79 a écrit:je ne vois pas du tout comment faire :/
solution analytique de l'exo
O : point dintersection des droites (CB) et (CB)
repère: (O,OC,CB) donc O(0,0) , C(1,0) , B(0,1) , A'(1,1) , B'(b,0) , C'(0,c) , A(b,c)
tu cherches les équations des droites (BB') et (CC') puis leur intersection. Tu vérifies que ce point d'intersection est aligné avce A et A'
rem: tu peux choisir un autre repère
Bonjour
Cet exercice relève de la géométrie projective.
Juste une remarque avec les vecteurs
[img][IMG]http://img685.imageshack.us/img685/9387/parall.png[/img][/IMG]
Si on pose U=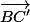 V=
V=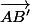 W=
W=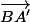 K=
K=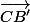
on remarque que
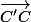 = W+V
= W+V
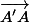 = K+U
= K+U
 = W+K+U+W
= W+K+U+W
donc =
= 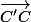 +
+ 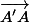
cela montre que si (AA') et (CC') sont parallèles, alors elles sont aussi parallèles à (BB')
si (AA') et (CC') se coupent en O, est-il possible de démontrer que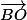 et
et  sont colinéaires, sans passer par la géométrie projective ???
sont colinéaires, sans passer par la géométrie projective ???
O serait-il le barycentre de B et B' avec certains coefficients ?
Cet exercice relève de la géométrie projective.
Juste une remarque avec les vecteurs
[img][IMG]http://img685.imageshack.us/img685/9387/parall.png[/img][/IMG]
Si on pose U=
on remarque que
donc
cela montre que si (AA') et (CC') sont parallèles, alors elles sont aussi parallèles à (BB')
si (AA') et (CC') se coupent en O, est-il possible de démontrer que
O serait-il le barycentre de B et B' avec certains coefficients ?
chan79 a écrit:Bonjour
Cet exercice relève de la géométrie projective.
Juste une remarque avec les vecteurs
[img][IMG]http://img685.imageshack.us/img685/9387/parall.png[/img][/IMG]
Si on pose U=V=
W=
K=
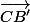
on remarque que
= W+V
= K+U
= W+K+U+W
donc=
+
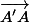
cela montre que si (AA') et (CC') sont parallèles, alors elles sont aussi parallèles à (BB')
si (AA') et (CC') se coupent en O, est-il possible de démontrer queet
sont colinéaires, sans passer par la géométrie projective ???
O serait-il le barycentre de B et B' avec certains coefficients ?
OUI forcément et la méthode la plus simple pour le voir est de choisir un bon repère
Pour une solution vectorielle, tu peux exprimer K en fonction de W et U en fonction de V.. etc..
mais je pense que ça reviendra à copier une solution analytique
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
