Bonjour,
je commence les constructions à la regle et au compas dans la théorie de Galois, c'est trés interessant mais j'ai qqls problemes dés le début :happy2:
Je rappelle l'énoncé et la premiere question (on verra pour les prochaines):
On dit que
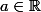
est
constructible à la regle et au compas s'il existe une suite d'extensions quadratiques

avec
 QUESTION 1:
QUESTION 1:Soit
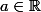
constructible à la regle et au compas.
Montrer que

est algébrique sur

.
Soit

le corps de décomposition du polynome minimal de

sur

.
Montrer que l'extension

est de degré une puissance de 2.
Mes (ébauches de) réponses:Il existe une suite d'extensions quadratiques

avec

.
Pour tout O<i<n on a

est de degré 2 donc algébrique (car extension finie). Par composition l'extension

est algébrique donc

est algébrique sur

.
Soit maintenant

le corps de décomposition du polynome minimal de

sur

.
J'appelle

les conjugués de

(compris

) . Alors L est le corps engendré par

et les

. (A-t-on une condition sur

?) Pour simplifier les écritures je pose m=2.
Put-on écrire
 \mathbb{Q}(a_2))
le sous-corps engendré par
 \cup \mathbb{Q}(a_2))
? Si oui alors
 \mathbb{Q}(a_2): \mathbb{Q}] = [\mathbb{Q}(a_1) : \mathbb{Q}] \times [\mathbb{Q}(a_2) : \mathbb{Q}])
pour

on a
 : \mathbb{Q}] = 2^m)
, où
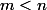
puisque
 \in K_n)
.
Par contre je n'arrive pas à le montrer pour son conjugué... pourquoi
 : \mathbb{Q}] = 2^p)
, où
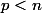
. A-t-on
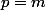
??
Une questionSi x est algebrique de degré d sur K alors K(x)/K est de degré d. La réciproque est-elle vraie??
mercii
