Two Galois Group Examples

[ortollj]

non mais il faut que je le revise d'abord, je vais regarder dans le livre de Jean-Paul Delahaye "merveilleux nombres premiers" ou je l'avais vu il y a quelque années.

[wserdx]

Désolé, en effet pour qu'il y ait un petit intérêt à ma formule, il faut expliciter le passage de à .
A on fait correspondre
soit solution de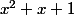, les trois racines de 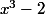sont
, et.
Les formules de passages sont alors




et inversement




donc si est l'inverse de




D'où en remplaçant on a explicitement les valeurs de en fonction de.

[ortollj]

Wserdx, quel interet trouves tu a inverser r et q dans la formule ?
rappel: abcdefghijklmnostuvwxyz
ca a l'air de marcher cela donne bien l'inverse .
faire un copy paste du code ci dessous dans la console Scilab.

Code: Tout sélectionner

x=poly(0,x) ;
p=round(rand()*14 -7);
q=round(rand()*14 -7);
r=round(rand()*14 -7);
function y=P(x)
y=p + q *x + r *x^2;
endfunction
j=%e^(2*%pi*%i/3);
α=2^(1/3);
pInv=(1/3)*( 1/P(α) + 1/P(α*j) + 1/P(α*j^2));
qInv=(1/(3*α))*( 1/P(α) + j/P(α*j) + j^2/P(α*j^2));
rInv=(1/(3*α^2))*( 1/P(α) + j^2 /P(α*j) + j/P(α*j^2));
Inv=pInv + qInv*α + rInv*α^2 ;
P(α)*Inv

[Ben314]

donc si est l'inverse de

Je t'avoue que je vois toujours pas bien l'intérêt par rapport par exemple à où .
Tu peut me montrer à quels calculs ça te conduit lorsque c'est à dire pour trouver l'inverse de ?

Sinon, perso, il me semble qu'à la main, le plus rapide pour trouver les coordonnées de l'inverse d'un élément, c'est quand même l'algo. d'Euclide.

[wserdx]

Oui en effet, c'est pareil que ta solution.
Les calculs donnent : (je ne les ai pas faits à la main, voir le code Magma plus bas...)
[Edit: j'ai rajouté l'application numérique]

Code: Tout sélectionner

    Q:=RationalField();
    P<a,j,p,q,r>:=PolynomialRing(Q,5);
    K:=quo<P|a^3-2,j^2+j+1>;
    u:=p+q*a+r*a^2;
    v:=p+q*a*j+r*a^2*j^2;
    w:=p+q*a*j^2+r*a^2*j;
    N:=K!(u*v*w);
    I:=K!(v*w);
    N;
    //p^3 - 6*p*q*r + 2*q^3 + 4*r^3
    I;
    //-a^2*p*r + a^2*q^2 - a*p*q + 2*a*r^2 + p^2 - 2*q*r
    Evaluate(N,[a,j,3,2,1]);
    //11
    Evaluate(I,[a,j,3,2,1]);
    //a^2 - 4*a + 5



[ortollj]

je crois que mon QI de poisson rouge me joue encore des tours
hier soir j'ai lu dans le bouquin de JP Delahaye "merveilleux nombre premier"
que quand on a fait la division Euclidienne de a/b alors,
cela permettait en remontant l'algo de division Euclidienne de trouver x et y de a*x+b*y=c du Th de Bezout
est ce que par hasard ce ne serait pas ca que tu voulais que je fasse ?.
si oui je le ferai ce soir

x^3 -2 /(x^2 + 2*x + 3) => D=x R= (x^3 -2)-(x^2 + 2*x + 3)*x=(-2*x^2 -3*x -2)
(x^2 + 2*x + 3)/(-2*x^2 -3*x -2) => D= -2 R=(x^2 + 2*x + 3)-((-2*x^2 -3*x -2)*-2)=-3*x^2- 4*x -1
(-2*x^2 -3*x -2)/(-3*x^2- 4*x -1)=> D=2/3 R=(-2*x^2 -3*x -2) -(-3*x^2 - 4*x -1)*(2/3)=-x/3-4/3=(-1/3)*(x+4)

[ortollj]

tentative bezout



11=( x^2 + 2*x + 3)-(x+4)*(x-2)
(x+4)=((x^3 -2)-(x^2 + 2*x + 3)*(x-2))
11=( x^2 + 2*x + 3)-((x^3 -2)-(x^2 + 2*x + 3)*(x-2))*(x-2)
11=( (x+4)*(x-2)+11)-((x^3 -2)-(x^2 + 2*x + 3)*(x-2))*(x-2)
0=( (x+4)*(x-2))-((x^3 -2)-(x^2 + 2*x + 3)*(x-2))*(x-2)
((x^3 -2)-(x^2 + 2*x + 3)*(x-2))*(x-2)=( (x+4)*(x-2))

(x^3 -2)*(x-2) - (x^2 + 2*x + 3)*(x-2)*(x-2)= (x+4)*(x-2)

c'est fou je n'arrive pas a retrouver l'egalité de ben314 ci dessous
qu'est ce qui ne va pas ?

[Ben314]

Oui, le principe, c'est bien ça.
Par contre, a mon avis, pour pas te paumer, tu as franchement intérêt à nommer les différents restes au fur et à mesure. Tu peut aussi le faire "en une seule passe" lors des calculs des restes :

1ére division :

2em division :




Maintenant, en prenant on a et on obtient
c'est à dire

Et, bien que ce soit évidement le même résultat, ce n'est pas directement la même chose que la formule qui est "plus théorique", c'est à dire qui permet d'avoir l'inverse d'un quelconque alors que de faire les division euclidiennes successives en partant d'un polynôme quelconque, c'est très chiant : il y a des tonnes de cas particuliers.
Bref, pour trouver l'inverse d'un élément particulier, le plus rapide est sans doute la méthode des divisions euclidiennes, mais si tu veut la formule générale donnant l'inverse d'un quelconque c'est pas la bonne méthode (par contre la méthode marche pour montrer qu'un quelconque (non nul) admet un inverse vu qu'on sait de façon théorique que Bézout est valable lorsque deux polynômes sont premiers entre eux)

[ortollj]

est t'il possible de demontrer que quelque soit


si on pose

alors on reconnait l'identité de Gauss

PS:qu'est ce que c'est que ces foutus <br>

[ortollj]

euh je voulais dire si (a , b ,c ne sont pas tous nul ) !

[Ben314]

Oui, c'est bien ça.
Et là, tu est en train de retrouver "à la main" un résultat bien connu, à savoir que le déterminant de ton système, c'est la "norme" de l'élément de départ, c'est à dire le produit de tout les conjugués de .
Ici,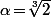 a pour polynôme minimal 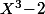dont les deux autres racines sont et (où ) donc les conjugués de sont et et tu peut vérifier que ton déterminant est en fait égal à

et donc qu'il est nul ssi p=q=r=0.
De même, si tu développe tu pourra vérifier que le que tu as obtenu, c'est

[ortollj]

Merci Ben314
je voudrais aussi dire que les videos de Matthew Salomone
Sommaire VideoMatthew Salomone
sont tres efficaces , il arrive a me faire comprendre des concepts abstraits.
et croyez moi, il a du merite !
je crois que si quelqu'un veut apprendre la Theorie de Galois ca me semble ideal
de les regarder dans un premier temps.
meme si il y a parfois des petites erreurs, mais les principes sont la.
(c'est pas evident de ne jamais faire d'erreur, il fait beaucoup de videos )
Compass and straight edge constructions
je vais maintenant essayer d'avancer dans le bouquin de Ian Stewart, et j'espere que j'arriverai a comprendre
cette Theorie de Galois. peut etre meme que quand j'aurais suffisament avancé (soyons fou !)
je retenterai le mooc de l'ENS: sur la theorie de Galois