Fractions irrationnelles

[victen]

Il m'est demandé de décomposer en facteur irreductible la fraction irrationnelle suivante :

X/(X^4+1)

J'ai simplement décomposé X^4+1 =>

X^4+1 = (X-e^ipi/4)(X-e^-ipi/4)(X-e^i3pi/4)(X-e^-i3pi/4) dans C(X)
X^4+1 = (X^2-V2X+1)(X^2+V2X+1) dans R(X)

j'ai donc écrit :

X/((X-e^ipi/4)(X-e^-ipi/4)(X-e^i3pi/4)(X-e^-i3pi/4)) est la decompo de X/(X^4+1) dans C(X)
X/((X^2-V2X+1)(X^2+V2X+1)) est la decompo de X/(X^4+1) dans R(X)

Merci de votre aide :we:

[busard_des_roseaux]

bonjour,
calculons les raacines de

elles vérifient

donc

dans le cas de quatre racine simples, on écrit

(1)

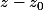
en multipliant , par exemple , par des deux cotés et

[victen]

Mais j'ai trouvé les racines de X^4+1 !

Ma question est : cela change t-il quelque chose de decomposer X/X^4+1 et decomposer de X^4+1 (mis a part que la decomposition de X^4+1 sera au denominateur) ?

[busard_des_roseaux]

Il y a une décomposition "théorique" que tu dois obtenir (dite "décomposition d'une fraction rationnelle en éléments simples". tu n'as pas de cours ? dans le temps , tout cela était expliqué dans le "Chambadal-Ovaert" d'analyse... mais ça c'était avant :we:

[victen]

Oui ! mais je voulais savoir si ma DES etait juste .. sinon quels sont les Pb ?
X/((X-e^ipi/4)(X-e^-ipi/4)(X-e^i3pi/4)(X-e^-i3pi/4)) est la decompo de X/(X^4+1) dans C(X)
X/((X^2-V2X+1)(X^2+V2X+1)) est la decompo de X/(X^4+1) dans R(X)

[busard_des_roseaux]

ah, oui... non ça parait faux ce que tu as écrit, une DES est une somme

[victen]

Donc comment m'y prendre autrement..?

[busard_des_roseaux]

dans le cas de quatre racine simples, on écrit

(1)

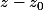
en multipliant , par exemple , par des deux cotés et
en faisant tendre

....................

[victen]

oui donc;

(a0/(X-e^ipi/4))+(a1/X-e^-ipi/4)+ (a2/(X-e^i3pi/4)+ (a3/(X-e^-i3pi/4)