Formule de Taylor avec reste intégral

par **Kyg** » 11 Aoû 2016, 17:01

Bonjour,

Je bloque sur un exercice où il s'agit de démontrer, via la formule de Taylor avec reste intégral, que :
Pour tout

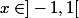
, la série de terme général

converge vers

.

Merci par avance pour votre aide.

par **zygomatique** » 11 Aoû 2016, 18:12

salut

et on continue avec des IPP ...

par **Robot** » 11 Aoû 2016, 19:56

La consigne est d'employer la formule de Taylor avec reste intégral. Tu suis donc la consigne en écrivant la formule de Taylor avec reste intégral pour la fonction

entre

et

. Tu t'attends à voir un certain rapport avec la série de terme général

pour

.
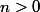
Après, tout le sel de l'exercice est dans la majoration du reste intégral.

Formule de Taylor avec reste intégral

Formule de Taylor avec reste intégral

Re: Formule de Taylor avec reste intégral

Re: Formule de Taylor avec reste intégral

Qui est en ligne