Formule des chaînes, dérivée seconde

[grecle]

Bonjour,

Révisant, j'ai trouvé ce problème :
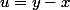
Soit . On pose et .

Montrer que l'on a :


Je ne pense pas que le problème soit très compliqué. Pour le résoudre j'ai commencé par écrire la formule des chaînes.

J'obtiens donc :



Après avoir effectué ceci, j'ai envie de dériver de nouveau ces équations, pour faire apparaitre des dérivés secondes...cependant je ne vois pas comment faire à cause des différentes variables.

Merci.

[GaBuZoMeu]

Ben on continue ...



etc.

PS. Il peut être commode de remarquer que et sont linéaires en et . Les dérivées partielles ne sont donc pas trop méchantes ...

[grecle]

Merci, je vais regarder cela rapidement.

Merci !

[GaBuZoMeu]

Avec plaisir.

[grecle]

Mmmh...je ne trouve pas le même résultat. Je commence donc par dériver mes deux lignes par rapport à x. A droite du égal je les dérive comme étant des produits. Je tombe bien ensuite sur la dérivée de f qui est déjà dérivé par rapport à u. Mais ce n'est pas un produit ?? Je ne comprends pas le résultat présenté..

Je vais ré essayer en attendant.

Merci bien

[GaBuZoMeu]

Je ne comprends pas tes états d'âme. Il n'(y a pourtant pas trop de questions à se poser !
Je te rappelle la remarque déjà faite que et sont linéaires en et , donc leurs dérivées partielles sont très simples et leurs dérivées partielles secondes encore plus simples !!