Probleme sur les chaines de markov

par **willy22** » 28 Juil 2006, 12:30

Bonjour
je ne vois pas comment resoudre cet exercice
pouvez vous m'aider s'il vous plait

On considere une chaine de markov finie de taille n, en temps discret, de matrice de transition P.

1. Rappeler les conditions que doivent vérifier les Pi,j afin que P soit une matrice de transition.
2. On suppose qu'il existe un réel positif b tels que:

quelque soit i 1..n,
quelque soit j 1..n-1,
Pi,j+1 = b Pi,j

Donner la distribution stationnaire de la chaine de markov ayant comme matrice de transition P.

Merci

par **Yipee** » 28 Juil 2006, 14:38

La reponse à la question 1 doit être dans ton cours non ? Il faut que la somme des coefficents de chaque ligne vaut 1

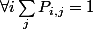
La réponse 2 est alors facile en utilisant cela.

par **willy22** » 28 Juil 2006, 14:50

Ben Merci de ta reponse mais je ne comprends toujours pas la 2e question

par **Yipee** » 28 Juil 2006, 16:06

Que ne comprends-tu pas ? Comment trouver P ou comment trouver la distribution stationnaire ?

par **jonath** » 28 Juil 2006, 16:20

comment trouver la distribution stationnaire?

par **jonath** » 28 Juil 2006, 16:32

la matrice P est de la forme
a b b
b a b
b b a
pour n = 3 par exemple

P possede une valeur propre égale a 1 associé au vecteur propre [ 1/n 1/n 1/n].

le vecteur propre est la distribution stationnaire cherchée

est ce que vous confirmez YIPEE ?

par **Yipee** » 29 Juil 2006, 14:42

La matrice P n'est pas de cette forme...

par **jonath** » 29 Juil 2006, 18:04

salut
ben ok
j ai essaye c tout
mais toi tu dois connaitre la solution ?

par **Yipee** » 29 Juil 2006, 18:16

Oui, je connais la solution. Pour tout i tu notes

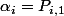
le premier coefficient de la ligne. Après tu as, d'après ta relation

Cela te donne la matrice P. Il est alors aisé de verifier que le vecteur (1,1,1,...,1) est un vecteur propre pour la valeur propre 1.

Probleme sur les chaines de markov

probleme sur les chaines de markov

Qui est en ligne