Bonjour,
Je reviens sur cette histoir d'anti-linéarité qui me travaille encore.
Le résultat principal de ce post est le suivant :
 = \mathcal{L}_k(E, \overline F))
Où
)
est l'ensemble des applications

-antilinéaires de

dans

et

est le k-espace vectoriel conjugué de

relativement à l'automorphisme de corps

Les applications

-antilinéaire sont donc des applications linéaires particulières. Ainsi, tous les théorèmes valables sur les applications linéaires restent vrais, d'autant que les espaces vectoriels et leurs conjugués et sont très ressemblants : mêmes familles libres, mêmes familles génératrices, mêmes bases, etc.
--- Rappels et notations ---
Je commence par rappeller quelques notions probablement connues de presque tous, mais qui permettent de mettre à plat les prérequis et les notations que j'utilise :
Soit

un corps commutatif,

un automorphisme de k (un morphisme de corps bijectif) et

et

deux

-espaces vectoriels.
On rappelle que
, +, \cdot))
est un

-espace vectoriel.
Soit
)
. On dit que f est additive si
 \in E^2, f(x + y) = f(x) + f(y))
On dit que

est une applicattion

-linéaire si elle est additive et si
 = \lambda f(x))
On dit que

est une application

-antilinéaire si elle est additive et si
 = \sigma(\lambda) f(x))
On note
)
l'ensemble des applications

-linéaires. C'est un sous-espace vectoriel de
)
On note
)
l'ensemble des applications

-antilinéaires.
-- Espace conjugué --
)
est un

-espace vectoriel
On considère le triplet
)
où si

et

,
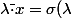 \cdot x)
Afin de ne pas confondre les deux structures, on notera
)
cette nouvelle structure et
)
la structure originale.
Ainsi,
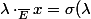 \cdot_E x)
Exemple :

est un

-espace vectoriel définie par
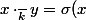 \cdot_k y)
. Ce n'est pas un corps en général.
Proposition : Soit

une application

-antilinéaire de

dans

.
Alors la fonction

est linéaire.
Corollaire : L’ensemble des applications

-antilinéaire de

dans

est
)
 = \mathcal{L}_k(E, \overline F))
Corollaire :
)
est un

-espace vectoriel.
-- Espace dual --
On note
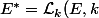)
l'ensemble des forme

-linéaires sur

.
On note
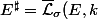)
l'ensemble des forme

-antilinéaires sur

.
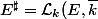)
-- Application sesquilinéaire --
Définition : Soit

une application.
On dit que f est

-sesquilinéaire si
 : F \longrightarrow G)
est

-antilinéaire
 : E \longrightarrow G)
est

-linéaire
On considère (enfin) la fonction

définie par :
)
 = f(\cdot, y))
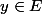
,
)
est linéaire :
 \in \mathcal{L}_k(E, G))

est

-antilinéaire
))
}))
On peut donc appliquer, entre autres, le théorème du rang à

Merci beaucoup, beaucoup de m'avoir lu.
Toutes les remarques, critiques, suggestions, ajouts sont les bienvenus !
Quand à moi je vais pouvoir continuer à explorer le monde magique de l'algèbre biilinéaire.
