Forme canonique dans un polynôme de degré 3
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
GoG
- Membre Naturel
- Messages: 35
- Enregistré le: 10 Aoû 2006, 00:59
-
par GoG » 19 Sep 2006, 19:59
Bonsoir à toutes et à tous.
On considère l'équation
 : ax^{3}+bx^{2}+cx+d = 0)
où
 \in\mathbb{R}*\times \mathbb{R}^3)
.
Montrez que
)
peut se ramener à une équation de la forme :
: x^3+px+q = 0)
où
 \in \mathbb{R}^2)
Je suis sûr qu'il s'agisse d'une forme canonique mais j'avoue ne pas réussir à y arriver...Si vous pouviez m'aider à la déterminer pour pouvoir répondre à cette question,je vous en remercierais.
Bonne soirée à toutes et à tous
A+,cordialement Gauthier
-
xon
- Membre Relatif
- Messages: 100
- Enregistré le: 24 Aoû 2006, 14:57
-
par xon » 19 Sep 2006, 20:09
salut,
alors déjà tu peux commencer par diviser par a puisqu'il est non nul.
->
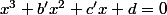
Ensuite tout vient de
^3=a^3+3a^2b+3ab^2+b^3)
en considérant que
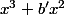
est le début du devellopement de
^3)
et en enlevant ce qu'il faut.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
