Fontion arctan(exp(x))
20 messages
- Page 1 sur 1
Fontion arctan(exp(x))
Bonjour a tous...
me voila avec un exercice avec lequel j'ai du mal... j'ai esaye de faire un peu mais bon j'ai beaucoup de doute...
Merci de votre aide des maitenant...
On considere la fonction réelle f definie par f(x) = arctan(exp(x))
a) Montrer que f est strictement croissant sur R.
-> Arctan est continue et croissant sur - PI / 2 et PI / 2 exclu
exp est aussi une fonction continue et croissant sur - infini + infinie
D'ou la fonction composé de deux fonction croissantes est croissante..
b) On note J=f(R), determiner l'intervalle
-> -pi/2, Pi/2
c) Montrer que f est une bijection de R sur J
-> Puisque f est strictement croissante + continue sur J alors bijection
d) Soit G : J -> R, l'application reciproque de f
Montrer que G est derivable en tout point de J
-> Arctan est continue et derivable sur son intervalle, de meme pour exp donc la fonction composé de deux fonctions derivable est derivable
e) Calculer G'(x)
-> (1/ 1+ x²) * exp(x) * exp(x)
f) Donner l'equation de la tangente au graphe C de G au point d'abscisse PI/4. Presicer la position de la tangente par rapport a C.
-> BLOQUEE
me voila avec un exercice avec lequel j'ai du mal... j'ai esaye de faire un peu mais bon j'ai beaucoup de doute...
Merci de votre aide des maitenant...
On considere la fonction réelle f definie par f(x) = arctan(exp(x))
a) Montrer que f est strictement croissant sur R.
-> Arctan est continue et croissant sur - PI / 2 et PI / 2 exclu
exp est aussi une fonction continue et croissant sur - infini + infinie
D'ou la fonction composé de deux fonction croissantes est croissante..
b) On note J=f(R), determiner l'intervalle
-> -pi/2, Pi/2
c) Montrer que f est une bijection de R sur J
-> Puisque f est strictement croissante + continue sur J alors bijection
d) Soit G : J -> R, l'application reciproque de f
Montrer que G est derivable en tout point de J
-> Arctan est continue et derivable sur son intervalle, de meme pour exp donc la fonction composé de deux fonctions derivable est derivable
e) Calculer G'(x)
-> (1/ 1+ x²) * exp(x) * exp(x)
f) Donner l'equation de la tangente au graphe C de G au point d'abscisse PI/4. Presicer la position de la tangente par rapport a C.
-> BLOQUEE
Par rapport à votre exercice.
Bonjour,
A la partie B de votre question, si on regarde de près :
 , c'est à dire :
, c'est à dire :
 , attention au fait que
, attention au fait que 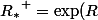)
 , donc
, donc 
De plus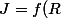=]0,+\frac{\pi}{2}[) car
car 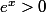
A la partie B de votre question, si on regarde de près :
De plus
f(x) = Arctan(exp(x))
Arctan est continue strictement croissante et dérivable sur r ........
De plus,
lim en + oo Arctan(e^x) = lim Arctan(x) = pi/2
et
Lim en - oo lim Arctan(e^x) = lim Arctan(x) = 0
f est donc une bijection de r sur ]0 ; +pi/2[
Sa bijection réciproque g va de ]0 ; +pi/2[ vers r.
g est dérivable car pour tout x in r , f'(x) dif 0
Voila ce que j'ai refait entre temps..
Arctan est continue strictement croissante et dérivable sur r ........
De plus,
lim en + oo Arctan(e^x) = lim Arctan(x) = pi/2
et
Lim en - oo lim Arctan(e^x) = lim Arctan(x) = 0
f est donc une bijection de r sur ]0 ; +pi/2[
Sa bijection réciproque g va de ]0 ; +pi/2[ vers r.
g est dérivable car pour tout x in r , f'(x) dif 0
Voila ce que j'ai refait entre temps..
En effet
En effet, c'est le principe de la fonction composée :



Ici F c'est exp et G c'est Arctan.
 ,
, (zone d'arrivé de F inter zone de "départ" de G).
(zone d'arrivé de F inter zone de "départ" de G).
et finalement ou plus précisément
ou plus précisément  .
.
En faisant les courbes ça devient plus clair.



Ici F c'est exp et G c'est Arctan.
 ,
, (zone d'arrivé de F inter zone de "départ" de G).
(zone d'arrivé de F inter zone de "départ" de G).et finalement
 ou plus précisément
ou plus précisément  .
.En faisant les courbes ça devient plus clair.
Pour la partie C (Montrer que f est une bijection),
Pour la partie C (Montrer que f est une bijection),
Si la fonction est une injection, alors
est une injection, alors ) est une bijection.
est une bijection.
Dans le cas de f(x), elle est (strictement) croissante, donc une injection de à
à  , donc une biection de
, donc une biection de  à J. A mon avis il est inutile d'utiliser l'argument de la continuité de f.
à J. A mon avis il est inutile d'utiliser l'argument de la continuité de f.
Si la fonction
Dans le cas de f(x), elle est (strictement) croissante, donc une injection de
oke.. je te remercie pour ton aide... tres sympa..
tu peux aussi m'aider sur la derniere question... en effet pour calculer l'equation tangente ainsi que la position.. il faut faire
le developpement limité a l'ordre 3 de cette fonction non ?
c'est ce que l'on m'a appris... par exemple
exp(x) = 1 + x + x²/2 +x'3/3
l'equation de la tangente est 1 + x
x²/2 etant positif alors C est au dessus de la tangente...
enfin je pense que c'etait une maniere de le faire.. mais avc la methode de mathelot je ne vois plus trop comment faire..
tu peux aussi m'aider sur la derniere question... en effet pour calculer l'equation tangente ainsi que la position.. il faut faire
le developpement limité a l'ordre 3 de cette fonction non ?
c'est ce que l'on m'a appris... par exemple
exp(x) = 1 + x + x²/2 +x'3/3
l'equation de la tangente est 1 + x
x²/2 etant positif alors C est au dessus de la tangente...
enfin je pense que c'etait une maniere de le faire.. mais avc la methode de mathelot je ne vois plus trop comment faire..
Reprendre en TeX
f(x) = Arctan(exp(x))
Arctan est continue strictement croissante et dérivable sur R
De plus,
} = \lim_{e^x \rightarrow + \infty} {Arctan(e^x)} = \pi/2) , ok.
, ok.
et
} = \lim_{e^x \rightarrow 0} {Arctan(e^x)} = 0) ,ok aussi.
,ok aussi.
Hmmm, je réfléchis, pour la dernière question ...
Pour la tangeante, c'est beaucoup plus simple!
D'abord il faut calculer x en fonction de y, car si) donc
donc 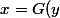) , à trouver.
, à trouver.
Après, vous pouvez changer la notation pour avoir :
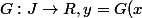) .
.
La tangeante c'est la dérivée de G au point donné , donc
, donc 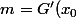) .
.
Après, sachant que la tangeante (qui est une droite), passe par le point)) , vous avez toutes les données pour construire l'équation de la droite.
, vous avez toutes les données pour construire l'équation de la droite.
Arctan est continue strictement croissante et dérivable sur R
De plus,
et
Hmmm, je réfléchis, pour la dernière question ...
Pour la tangeante, c'est beaucoup plus simple!
D'abord il faut calculer x en fonction de y, car si
Après, vous pouvez changer la notation pour avoir :
La tangeante c'est la dérivée de G au point donné
Après, sachant que la tangeante (qui est une droite), passe par le point
L'énoncé
Si j'ai bien compris, on demande de donner l'equation de la tangente au graphe C de G au point d'abscisse  puis de presicer la position de la tangente par rapport a C.
puis de presicer la position de la tangente par rapport a C.
Les développements limités ici mènent à la même réponse...numériquement.
Vous avez trouvé que : = \frac{e^x}{1+e^{2x}}) , avec les DL
, avec les DL  . Ce qui donne :
. Ce qui donne :
 = \frac{1+x}{1+(1+2x)} = \frac{1}{2}) , donc
, donc 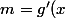 = \frac{1}{f^{\prime}(x)} = 2) .
.
Numériquement, c'est la même réponse, mais la méthode indiquée plus haut est utlisée au lycée. Elle me semble plus simple et plus précise.
Les développements limités ici mènent à la même réponse...numériquement.
Vous avez trouvé que :
Numériquement, c'est la même réponse, mais la méthode indiquée plus haut est utlisée au lycée. Elle me semble plus simple et plus précise.
en effet j'essaye de calculer G'(x) je trouve des resultats differents sans arret...
comme e(x) / 1 + e (x) ²
ou encore (1 / tan² )* e(x)²
je ne sait pas laquelle et la bonne... J'ai fait 2 methodes differentes et jai deux resultat differrent plus le resultat de la personne qui a poster avant ca m'en fait 3 .. perdu :S
Oui pour la tengente je trouve bien cela de plus la courbe est au dessus de C... car nous avons une valeurs positives pour les termes en x²...
merci énormement pour ton aide... et puis pour G'(x) j'ai oublier de mettre les resultats sur 1... donc j'ai f'(x)... et G'(x) = 1 / f'(x)...
comme e(x) / 1 + e (x) ²
ou encore (1 / tan² )* e(x)²
je ne sait pas laquelle et la bonne... J'ai fait 2 methodes differentes et jai deux resultat differrent plus le resultat de la personne qui a poster avant ca m'en fait 3 .. perdu :S
Oui pour la tengente je trouve bien cela de plus la courbe est au dessus de C... car nous avons une valeurs positives pour les termes en x²...
merci énormement pour ton aide... et puis pour G'(x) j'ai oublier de mettre les resultats sur 1... donc j'ai f'(x)... et G'(x) = 1 / f'(x)...
Pas de panique
Regardez les formules de mathelot à la page précédente, vous y trouverez la formule de y=G(x).
De mon côté j'ai fait les calculs, j'ai le même résultat avec les deux méthodes.
Mais il est minuit 40 ! La fatigue et le fait de rester sur un seul exercice longtemps embrouille les pistes (je parle d'expérience :we: ).
Reposez-vous et puis recommencer l'esprit clair demain matin, vous verrez que ce n'est pas si difficile que ça.
Bon travail.
Mathématiquement votre.
De mon côté j'ai fait les calculs, j'ai le même résultat avec les deux méthodes.
Mais il est minuit 40 ! La fatigue et le fait de rester sur un seul exercice longtemps embrouille les pistes (je parle d'expérience :we: ).
Reposez-vous et puis recommencer l'esprit clair demain matin, vous verrez que ce n'est pas si difficile que ça.
Bon travail.
Mathématiquement votre.
oui depuis le post que j'avais laisser la premiere fois j'ai vu enormement de changement... mais j'ai un DS pas tres longtemps d'ici donc jprefre comprendre vraiment ces exo car ces des exos typique pour les examens... et puis merci encore... je meterai le dernier pooint demain c'est promis ^^
bonne nuit.. et puis desolé pour le temps que j'ai pris...
bonne nuit.. et puis desolé pour le temps que j'ai pris...
mrc a écrit: je metterai le dernier point demain c'est promis ^^
on raisonne avec deux noms de variables x et y bien distinctes
x prend ses valeurs dans l'ensemble de définition de f
y prend ses valeurs dans l'ensemble de définition de g
certains couples
Equation de la tangente à
Le point
le coefficient directeur de la tangente en A à
Le point
le coefficient directeur de la tangente en A' à
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
