Fonctions holomorphes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ifkirne
- Messages: 8
- Enregistré le: 02 Mai 2012, 17:18
-
 par Ifkirne » 02 Mai 2012, 19:48
par Ifkirne » 02 Mai 2012, 19:48
Bonjour tout le monde,
J'ai besoin de votre aide pour la résolution de la dernière question (2-b) de l'exercice suivant:
Soit

un ouvert connexe de

et

une fonction holomorphe sur

.

et

sont respectivement la partie réelle et la partie imaginaire de

. On suppose qu'il existe

tels que

,
+aQ(z)+b=0)
.
1. Montrer que [CENTER]

,
=0)
.[/CENTER]
2.(a) Soit
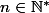
. Montrer que
[CENTER]

,
}(z)=0)
.[/CENTER]
(b) Soit

. En déduire qu'il existe un réel

tel que
[CENTER]
)
,
=f(z_0))
.[/CENTER]
Merci d'avance.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 02 Mai 2012, 20:03
par girdav » 02 Mai 2012, 20:03

est localement une série entière, et seul le premier terme est non nul. Donc

est localement constante. Par connexité, elle l'est partout.
-
Ifkirne
- Messages: 8
- Enregistré le: 02 Mai 2012, 17:18
-
 par Ifkirne » 02 Mai 2012, 20:16
par Ifkirne » 02 Mai 2012, 20:16
Merci beaucoup pour votre réponse.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités