Fonctions holomorphes

[mehdi-128]

Bonjour,

comment montrer :

Soit U un ouvert borné convexe.f:U->R est harmonique sur U et continue sur U barre.(adhérence)
Montrer que f atteint son min sur U barre et que:
Min (z de U barre)f(z)=min(z de U) f(z)

Ensuite: soit : G:C->C ou :g(z)=exp(z)-exp(z barre)

soit:f=(1/2) */G/

1/ G est-elle holomorphe? (aucune idée)

2/f est-elle harmonique ? (ca dépend de G)

3/Donner une conjuguée harmonique de f sur {z de C/Im(z) c [0,Pi/2]
(comprends pas la question)

4/Calculer min f sur le triangle rectangle de sommets:i.Pi/4 , 1+i.Pi/2 ,iPi/2
(completement percu)


Ca serait sympa de me donner quelques indications ....

[tize]

Ca serait sympa de me donner quelques indications ....

bonjour,
Il me semble bien que si f est harmonique alors elle est continue, de plus est bornée dans donc est compact; une fonction continue sur un compact...
Ensuite, si le min est atteint sur alors c'est réglé, sinon c'est en mais il existe alors une suite de : et la continuité de f permet de conclure : inf sur U = inf sur U barre...
, G est donc à valeurs dans or une fonction holomorphe non constante est ouverte donc...

2) il n'y a plus qu'à trouver le Laplacien de f en fonction de y dans [0;pi] (mod 2pi) ou pas...

[mehdi-128]

bonjour,
Il me semble bien que si f est harmonique alors elle est continue, de plus est bornée dans donc est compact; une fonction continue sur un compact...
Ensuite, si le min est atteint sur alors c'est réglé, sinon c'est en mais il existe alors une suite de : et la continuité de f permet de conclure : inf sur U = inf sur U barre...
, G est donc à valeurs dans or une fonction holomorphe non constante est ouverte donc...

2) il n'y a plus qu'à trouver le Laplacien de f en fonction de y dans [0;pi] (mod 2pi) ou pas...

Merci pour ces réponses mais je ne connais pas les fonctions holomorphes ouvertes ? :hein:
Je dirai que comme exp(z barre )n'est pas H ,G n'est pas H....

Et je vois pas comment vous passez de z_n ->z_0 et f continue a :

inf sur U = inf sur U barre...

[tize]

Bonjour,
d'accord avec n'est pas holomorphe.
il existe tel que et puisque es dans l'adhérence il existe alors une suite de telle que et comme est continue et donc

[mehdi-128]

Bonjour,
d'accord avec n'est pas holomorphe.
il existe tel que et puisque es dans l'adhérence il existe alors une suite de telle que et comme est continue et donc

Ah Ok merci ,c'est ce que je pensait en gros mais j'étais pas sur ...


Avec les 2 cas ,j'obtiens que f est harmonique car le laplacien est nul ....

[tize]

Oui c'est bien ça :we:

[mehdi-128]

Oui c'est bien ça :we:

J'ai fais la 3,j'obtiens: Im(F)=-exp(x).cos(y) ou f=Re(F) avec F harmonique.

Mais je bloque pour cette question:

4/Calculer min f sur le triangle rectangle de sommets:i.Pi/4 , 1+i.Pi/2 ,iPi/2

[tize]

Bonjour,
il suffit de regarder le min sur chacun des côtés du triangle....

[mehdi-128]

Bonjour,
il suffit de regarder le min sur chacun des côtés du triangle....

Ah oui j'aimerai bien savoir comment on calcule le min sur un côté d'un triangle ....

Je dirai que le minimum est 1 soit exp(0) ....

[tize]

Si j'ai bien compris le triangle est le suivant :
le plus petit côté : (0,y) avec y dans [pi/4;pi/2]
l'autre côté de l'angle droit : (x,pi/2) avec x dans [0;1]
et l'hypoténuse : (x,y) avec y=pi/4*(x+1)
dans chaque cas il ne doit pas être trop difficile de calculer le min de
[edit] je dirai plutôt que le minimum est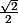 atteint en