Night: pour les fonctions dérivables sur R, c est faux. si f_1 est nulle sur R- non nulle sur R+ et f_2 nulle sur R+ non nulle sur R-, alors le Wronskien associé à f_1 et f_2 est identiquement nul, et ya pourtant pas de CL de f_1 et f_2 identiquement nulle.
Ben: bien joué ta démo marche ( bien qu'écrite de manière un peu lacunaire^^)
Ma demo à moi:je regarde la matrice comme étant à coeff dans le corps des fonctions méromorphes sur U. Comme le determinant est nul, l algebre linéaire nous dit qu il existe une combianaison linéaire des lignes qui est nulle à coeff dans le corps fonctions méromorphes. Autrement dit il existe p fonctions méromorphes
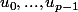
(non toutes nulles) telles que toutes les
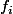
sont solutions de l équa diff (complexe)
}=0)
Ensuite on fixe z_0 qui n est pas un pole ni un zéro des
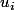
(on compte pas les u_i identiquement nul ), on prend des complexes
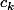
tels que
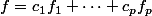
ait toutes ses dérivées d'ordre <p-1 nulles en

, puis comme f vérifie encore l'équa diff, on vérifie par une reccurence immédiate que toutes les dérivées de f en

sont nulles et donc que f=0 ( En fait on vérifie que l unicité de Cauchy Lipchitz marche encore pour une équa diff complexe )
