Fonctions cube et racine cubique - bijection et inverse

[adexvectorquantic]

Bonjour,

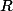
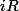
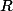
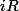
En partant de la courbe de la fonction carré restreinte à et (où on remarque que la courbe est en selle de cheval : une parabole croissante pour et une parabole décroissante pour ), je me suis posé des questions sur la fonction .

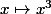
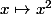
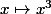
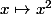
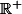
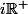
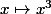
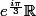
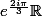
Premièrement, on remarque que a plans où les valeurs de la fonction sont réelles, alors que a exactement plans (où les valeurs de la fonction sont réelles). On remarque de plus, que pour on ne peut obtenir une bijection qu'en restreignant le domaine de définition à (ou ). Tandis que pour on obtient une bijection en restreignant le domaine à (ou bien ou bien ). 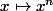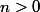J'ose avancer la conjecture suivante : pour avec , si est pair, alors on peut obtenir une bijection en restreignant le domaine de la fonction à un demi-plan (à choisir entre plusieurs demi-plans) et si est impair, on peut obtenir une bijection en restreignant le domaine de la fonction à un plan (à choisir possiblement entre plusieurs plans).

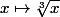
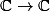
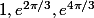
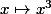
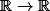
Si je comprends bien la fonction n'est pas une fonction sur car elle associe à trois différentes valeurs à la fois : . Mais la fonction étant bijective sur , il doit bien exister une fonction inverse. La fonction racine cubique étant le meilleur candidat pour cela, je me demande comment on oblige la fonction racine cubique à être une fonction ? 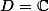Je suppose que on le fait en restreignant le domaine d'arrivé de la fonction racine cubique, mais comment peut-on restreindre un domaine d'arrivée à quelque chose de plus petit que (où est le domaine définition de la fonction)?



Merci et bonne journée