Equation avec racine cubique

[adamNIDO]

Bonjour,





pour la question 1:



pour la question 2:

j'arrive pas le résoudre

merci pour votre attention

[jonses]

Bonjour,





pour la question 1:



pour la question 2:

j'arrive pas le résoudre

merci pour votre attention

Pour la 1)

Pour

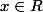
est dans le domaine de définition de (1)
si et seulement si : et

si et seulement si : et

si et seulement si :

Pour la 2)

1 et 0 ne sont pas solutions de (1), donc si on avait une solution à (1) elle est dans ]0,1[

[adamNIDO]

merci beaucoup jonses

[chan79]

Bonjour,

pour la 1, je dirais que 1-x² doit être positif ou nul car 6 est pair

D=[-1;1]

pour la 2, les nombres 0 et 1 ne sont visiblement pas des solutions

S'il y avait une solution strictement négative ,

[adamNIDO]

pour la 1, je dirais que 1-x² doit être positif ou nul car 6 est pair

D=[-1;1]

pour la 2, les nombres 0 et 1 ne sont visiblement pas des solutions

S'il y avait une solution strictement négative ,

donc la bonne réponse c'est que grâce a paire

pour la 2:
vous avez pris avec

ce qui vous donnez

[deltab]

Bonjour.

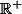
Juste une remarque, les fonctions énièmes sont définies sur pour n impair et sur pour n pair.
De plus, il ne faut confondre les fonctions racines énièmes avec les fonctions puissances , elles ne coïncident que sur

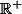
[adamNIDO]

Bonjour.

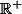
Juste une remarque, les fonctions énièmes sont définies sur pour n impair et sur pour n pair.
De plus, il ne faut confondre les fonctions racines énièmes avec les fonctions puissances , elles ne coïncident que sur

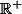
merci beaucoup

mais dans notre cas on est dans les fonctions puissances donc d’après vous Monsieur
quelle est le domaine de définition qui est correct [0,1] ou bien [-1;1] ?

[deltab]

merci beaucoup

mais dans notre cas on est dans les fonctions puissances donc d’après vous Monsieur
quelle est le domaine de définition qui est correct [0,1] ou bien [-1;1] ?

la fonctions est définie sur (3 est impair) donc les fonctions et sont définies sur \mathbb{R}
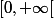
La fonction est défini sur ( 6 est pair) donc est définie sur [-1,1].
L'expression

[zygomatique]

Bonjour,





pour la question 1:



pour la question 2:

j'arrive pas le résoudre

merci pour votre attention

salut

élève au cube en n'oubliant pas que

puis réfléchis ....

[deltab]

merci beaucoup

mais dans notre cas on est dans les fonctions puissances donc d’après vous Monsieur
quelle est le domaine de définition qui est correct [0,1] ou bien [-1;1] ?

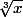
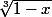
la fonction est définie sur (3 est impair) donc les fonctions et sont définies sur \mathbb{R}
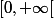
La fonction est défini sur ( 6 est pair) donc est définie sur .
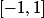
L'expression est donc définie sur .
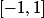
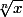
Je voulais attirer votre attention sur le domaine de définition de pour impair.

[zygomatique]

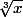
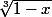
la fonction est définie sur (3 est impair) donc les fonctions et sont définies sur \mathbb{R}
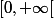
La fonction est défini sur ( 6 est pair) donc est définie sur .
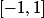
L'expression est donc définie sur .
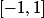
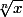
Je voulais attirer votre attention sur le domaine de définition de pour impair.

oui c'est cela ...

[adamNIDO]

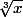
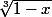
la fonction est définie sur (3 est impair) donc les fonctions et sont définies sur \mathbb{R}
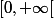
La fonction est défini sur ( 6 est pair) donc est définie sur .
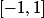
L'expression est donc définie sur .
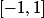
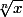
Je voulais attirer votre attention sur le domaine de définition de pour impair.

merci beaucoup mais le Domaine de defintion de l'equation 1 est :

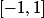
ou

[Ingrid55]

euh.. désolé pour la curiosité mais ton avatar @adamNIDO représente en fait quel écrivain ? ( en tout cas , j'ai déjà vu ce portrait dans un livre ...)

[deltab]

Bonsoir

merci beaucoup mais le Domaine de defintion de l'equation 1 est :

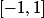
ou

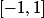
L'expression régissant l'équation est définie dans, la solution de l'équation elle est dans

[adamNIDO]

Bonsoir

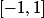
L'expression régissant l'équation est définie dans, la solution de l'équation elle est dans

merci beaucoup