Fonctions continues par morceaux

[Georges10]

Bonsoir à tous,

Soit f une fonction continue par morceaux sur [a, b], alors il existe deux suites de fonctions g_n et h_n telles que pour tout n >= 1, on ait

a) gₙ(t) ≤ g(_ₙ+1)(t) ≤ f(t) ≤h(ₙ_+1)(t) ≤ hₙ(t)

Voilà, j'aimerais savoir comment demontrer cela ( des pistes )

Merci d'avance !

[LB2]

Bonsoir,

tu as pas oublié un bout de l'énoncé? Quelles sont les propriétés vérifiées par g_n et h_n?

Parce qu'en l'état c'est un peu débile... tu prend g_n=f-1/n, h_n=f+1/n par exemple
Sinon pour faire les indices en latex tu tapes f_{n}

[Georges10]

Bonsoir à tous,

Soit f une fonction continue par morceaux sur [a, b], alors il existe deux suites de fonctions g_n et h_n telles que pour tout n >= 1, on ait

a)[gₙ(t) ≤ g_{n+1}(t) ≤ f(t) ≤h(ₙ_+1)(t) ≤ hₙ(t)


Voilà, j'aimerais savoir comment demontrer cela ( des pistes )

Merci d'avance !

b) 0 ≤ h_{n}{t} - g_{n}{t} ≤ 1\n

[Ben314]

Salut,
Je vois pas bien ce que tu as changé dans ton énoncé, plus précisément où as-tu répondu à la 1ère question de LB2 qui te montre que, tel quel, l'énoncé est complètement débile ?
Et encore, il est gentil avec toi concernant l'exemple qu'il donne de solution débile vu qu'il y a encore plus débile :
Si on prend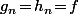 pour tout , ça vérifie encore plus trivialement toutes les condition que tu donne :
est vrai car
est vrai car