Bonjour,
J'ai un devoir maison avec lequel j'ai du mal qui porte sur la fonction de Weiertrass (prépa), on y définit une fonction φ de R dans R égale à la valeur absolue sur [-1;1],
puis pour n dans N et x dans R on pose φn(x) = φ(6^n*x)/2^n et fn la somme des φk pour k allant de 0 à n.
La première partie demandait d'utiliser un logiciel pour modéliser les courbes des différentes fonctions, aucun problème, dans la deuxième on s'attache à définir la fonction et à montrer sa continuité et c'est là que j'ai des ennuis.
La première question demande de montrer que pour tout x dans R la suite (fn(x)) avec n dans N est croissante et converge. Aucun problème pour montrer qu'elle est croissante, mais majorée (donc convergente) j'ai plus de mal. J'ai pris plusieurs exemples avec des valeurs de x et de n différentes mais je bloque à partir de là.
Fonction de Weierstrass
9 messages
- Page 1 sur 1
Re: Fonction de Weierstrass
Bonjour
Ta fonction est mal définie!
est mal définie!
C'est clair que les fonctions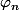 sont majorée par
sont majorée par 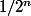 donc la suite
donc la suite )_n) est majorée.
est majorée.
Ta fonction
C'est clair que les fonctions
Re: Fonction de Weierstrass
Ensuite il s'agit de prouver que la fonction est continue sur R donc en substance de fixer un a dans R et de montrer que f est continue en a.
Re: Fonction de Weierstrass
f est la limite uniforme d'une suite de fonction continue donc f est continue.
Re: Fonction de Weierstrass
Il y a un suivi de questions, on fixe a dans R et on veut prouver que f est continue en a, ainsi on donne la limite de la fonction notée =\sum_{k=0}^{+\infty }{\frac{\varphi (6^kx)}{2^k}}) et on veut prouver que
et on veut prouver que  - f(a)|\leq (\sum_{k=0}^{n}{\frac{1}{2^k}|\varphi (6^kx)-\varphi (6^ka)|})+\frac{1}{2^{n-1}}) pour tout n dans N*.
pour tout n dans N*.
J'en suis rendu à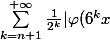-\varphi (6^ka)|}\leq \frac{1}{2^{n-1}}) mais je ne vois pas la fin.
mais je ne vois pas la fin.
J'en suis rendu à
Re: Fonction de Weierstrass
Je ne vois pas pourquoi on (re)passe par là. Est-ce que tu sais ce qu'est une limite uniforme?
Re: Fonction de Weierstrass
Je me suis renseigné sur le sujet oui, mais on n'a pas du l'aborder dans le cours, ce pourquoi il n'y a aucune mention de convergence uniforme dans le devoir même si ça semble illogique.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
